伏格爾法,經濟學名詞,又稱差值法。
基本介紹
- 中文名:伏格爾法
- 外文名:Vogel Method
- 別稱:差值法
- 領域:經濟學
什麼是伏格爾法,伏格爾法的步驟,伏格爾法實例分析,
什麼是伏格爾法
最小元素法的缺點是,為了節約一處的費用,有時造成在其他處要多花幾倍的運費。伏格爾法又稱差值法,該方法考慮到,某產地的產品如不能按最小運費就近供應,就考慮次小運費,這就有一個差額。差額越大,說明不能按最小運費調運時,運費增加越多。因而對差額最大處,就應當採用最小運費調運。
伏格爾法的步驟
伏格爾法一般能得到一個比用西北角法和最小元素法兩種方法所得的初始基本可行解更好的初始基本可行解。伏格爾法要求首先計算出各行各列中最小的cij,與次小的cij之間的差的絕對值,在具有最大差值的那行或列中,選擇具有最小的cij的方格來決定基變數值。這樣就可以避免將運量分配到該行(或該列)具有次小的cij的方格中,以保證有較小的目標函式值。所以,伏格爾法的基本步驟如下。
1、算出各行各列中最小元素和次小元素的差額,並標出差額最大的(若幾個差額同為最大,則可任取其一)。
2、在差額最大的行或列中的最小元素處填上儘可能大的數。
3、對未划去的行列重複以上步驟,直到得到一個初始解。
伏格爾法實例分析
例:某公司有三個加工廠A1,A2,A3 生產某產品,每日的產量分別為7T,4T,9T,該公司把這些產品分別運往四個銷售點B1,B2,B3,B4,各銷售點的每日銷量分別為3T,6T,5T,6T。從各工廠到各銷售點的單位運價如表1所示。問該公司如何調運產品,才能在滿足各銷售點需要量的前提下,使總費用最少?
表1:
B1 | B2 | B3 | B4 | |
A1 A2 A3 | 3 1 7 | 11 9 4 | 3 2 10 | 10 8 5 |
第一步:求各行各列最小和次小元素的差值。
在表2中,各行的差值分別為0,1,1,各列的差值分別為2,5,1,3。可見第二列差值最大,首先考慮第二列,在第二列中最小的cij 為c32=4,令x32=min{6,9}=6,填入表5-10 中,第二列飽和,划去該列。
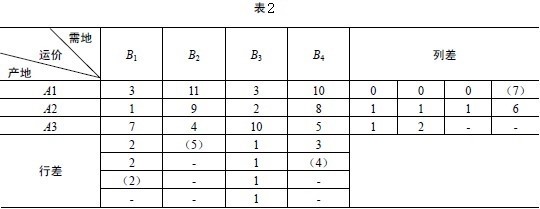 表2
表2第二步:求餘下的各行各列最小和次小元素的差值。
對剩下的方格重新計算各行各列的差值,各行差值分別為0,1,2,各列差值分別為2,1,3,第四列差值最大,在第四列中,最小的cij為c34 = 5,令x34=min{6,9-6}=3,於是第三行飽和,划去第三行。
第三步:重複上述過程。
可得其他基變數的值為:x21 = 3,x13 = 4,x23 = 1,x14 = 3。見表3。
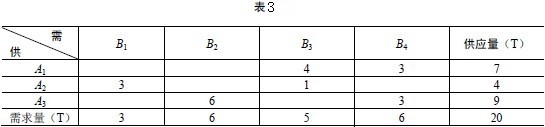 表3
表3此例的解所對應的 Z=1×3+4×6+3×5+10×2+8×1+5×3=85。
