人工變數(artificial variable)亦稱人造變數.求解線性規劃問題時人為加入的變數。
基本介紹
- 中文名:人工變數
- 外文名:artificial variable
- 求解方法:大M法、兩階段法
定義
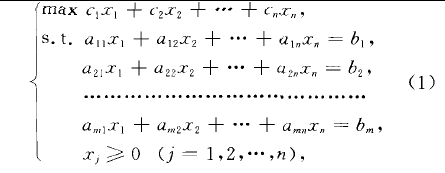
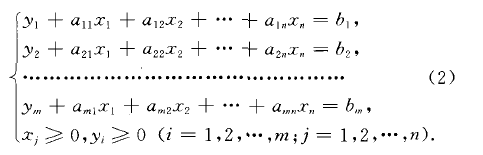

人工變數的作用
新LP與原LP的最優解
求解新LP的兩種方法
1.大M法

2.兩階段法








人工變數(artificial variable)亦稱人造變數.求解線性規劃問題時人為加入的變數。
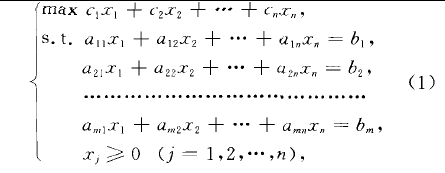
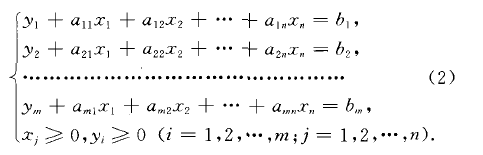










人工變數(artificial variable)亦稱人造變數.求解線性規劃問題時人為加入的變數。定義人工變數(artificial variable)亦稱人造變數.求解線性規劃問題時人為加入的變數.用單純形法求解線性規...
線上性規劃問題的單純形法中,若標準化後找不到單位矩陣,可以採用人造基,給方程加入人工變數後,用大M法和兩階段法處理求解。是求解線性規劃問題的一種方式。定律定義 其公式如下: → ,其中Xₛ是xₛ鬆弛變數組成的向量。正如上式所展示的那樣,所有約束是(≤),並且有非負右端項(b≥0)的線性規劃,...
虛擬變數簡介 虛擬變數又稱虛設變數、名義變數或啞變數,用以反映質的屬性的一個人工變數,是量化了的質變數,通常取值為0或1。引入啞變數可使線形回歸模型變得更複雜,但對問題描述更簡明,一個方程能達到倆個方程的作用,而且接近現實。例如,反映文程度的虛擬變數可取為:1:本科學歷;0:非本科學歷 一般地,在...
指示變數(indicator variables)又稱為虛擬參數(dummyparameter,D)、啞變數、啞元變數、虛擬變數等,是—-種用來表示品質變數且取值只為0和1或其他編碼形式的人工變數。基本介紹 定義 指示變數可以用來解釋計量經濟模型中的定性因素。它們經常被稱為虛擬、二元或二分變數,因為它們通常只取1或0兩個值,表示某種特徵的...
3.5人工變數法 3.5.1大M法 3.5.2兩階段法 3.6退化情形 3.6.1循環現象 3.6.2攝動法 3.7修正單純形法 第4章線性規劃對偶理論 4.1對偶問題的提出 4.2原問題與對偶問題的關係 4.2.1對稱形式的對偶問題 4.2.2非對稱形式的對偶問題 4.2.3一般情形 4.3對偶問題的基本定理 4.4對偶單純形法 4....
大M法(big M method)是線性規劃問題的約束條件(=)等式或(≥)大於型時,使用人工變數法後,尋找其初始基可行解的一種方法。定律定義 線上性規劃問題的約束條件中加人工變數後,要求在目標函式中相應地添加認為的M或一M為係數的項。在極大化問題中,對人工變數賦於一M作為其係數;在極小化問題中,對人工變數...
兩階段法(two-phase method)是尋找線性規劃問題初始基可行解的一種方法,把增加人工變數的線性規劃問題分為兩個階段去求解。第一階段主要是為了得到原問題的一個基本可行解,第二階段是在第一階段得到的基本可行解的基礎上求解原線性規劃問題。發展簡史 大M法與兩階段法都是在原問題缺少初始可行基的情況下利用引人...
原始-對偶方法的基本思想是為了得到原問題的基礎容許解,常用的方法是首先在原問題中引入人工變數,將目標函式換成人工變數之和的負值;然後極大化目標函式,並將得到的最優基礎容許解消去人工變數,此解即為原問題的基礎容許解,如果對偶問題有容許解與原問題的基礎容許解滿足互補鬆弛條件,則原問題的基礎容許解也就...
用人工變數法求解線性規劃問題時,在最終表中當所有cj-zj≤0,而在其中還有某個非零人工變數,這時最終表所得的結果就是絕對最優解。性質 他具有以下幾個特點:1、絕對最優解中必含有非零的人工變數。2、絕對最優解必對應於無窮多最優解的情形。3、絕對最優解不是原問題的最優解,但是所有的最優解都將在...
1.4 人工變數與兩階段法 第2章 非線性規劃 2.1 非線性規劃問題舉例 2.2 基礎知識 2.2.1 梯度 2.2.2 凸集 2.2.3 凸函式 2.3 無約束問題的最優解 2.4 有等式約束問題的最優解 2.5 有不等式約束問題的最優解 2.6 無約束問題的近似解法 2.6.1 梯度法 2.6.2 牛頓法 2.7 有...
