指示變數

指示變數(indicator variables)又稱為虛擬參數(dummyparameter，D)、啞變數、啞元變數、虛擬變數等，是—-種用來表示品質變數且取值只為0和1或其他編碼形式的人工變數。

基本介紹

• 中文名：指示變數
• 外文名：indicator variables
• 別稱：虛擬參數、啞變數、虛擬變數等
• 所屬學科：數學
• 所屬問題：數理統計
• 相關問題：回歸分析，計量經濟模型等

基本介紹

定義

指示變數可以用來解釋計量經濟模型中的定性因素。它們經常被稱為虛擬、二元或二分變數，因為它們通常只取1或0兩個值，表示某種特徵的存在與否或者某種條件的真假。它們也被稱為虛擬變數，表示我們為一個定性的、非數值特徵創建了一個數值變數。我們交替地使用指示變數和虛擬變數。將這些變數定義為0或1雖是任意的，但是我們會看到，這是非常方便的。一般地，我們定義一個指示變數D為：

舉例分析

為了使問題明確化，我們舉一個房地產經濟學中的例子。房屋的買方和賣方、估稅員、房地產估價者和抵押貸款銀行家都對預測房屋的現行市場價值感興趣。預測房價價值的一個常見方法是運用特徵價格模型，其中房價被解釋為房屋特徵（如房屋的大小、地點、臥室數量和房齡等等）的函式。其思路是將一個主體分成若干個組成部分，然後估計其每個特徵的價值。

現在，我們假設房屋的大小SQFT(以平方英尺為計量單位)是決定房價PRICE的唯一相關變數。設定的回歸模型為：

在該模型中，是居住面積每增加1平方英尺增加的房屋價值，是土地本身的價值。

在房地產領域，最重要的三個詞是“地點、地點和地點”。我們如何考慮房產位於理想地區（如在大學或者高爾夫球場附近）的影響？按這樣的方式思考，地點是房屋的“定性”特徵。

對於房價模型，我們可以定義一個指示變數來考慮房屋是否位於理想的地區，如：

指示變數能夠被用來捕捉模型的截距、斜率或者兩者同時的變化。我們將依次討論這些情況。

截距指示變數

指示變數的最常見套用是修正回歸模型的截距參數。將一個指示變數D以及一個新的參數引入回歸模型，我們得到：

將指示變數D引入回歸模型的影響能夠通過檢驗兩個地區的回歸函式E(PRICE)得到最好的說明。如果公式(3)的模型設定正確，則E(e)=0，且

在理想的地區，D=1，回歸函式的截距為。在其他地區，回歸函式的截距僅為。假設，這種差異可用圖1來描述。

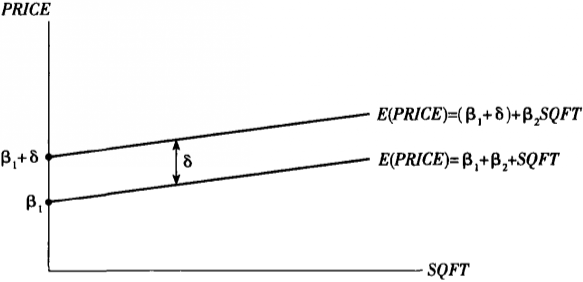圖1 截距指示變數

把指示變數D加入回歸模型，會導致關係平行移動。在房價模型中，參數的解釋為“位置溢價”，即由於房屋位於理想地區帶來的房價差異。指示變數D被引入回歸模型以表示某個定性因素造成的截距移動，被稱為截距指示變數或截距虛擬變數。在房價的例子中，我們預計位於理想地點的房屋價格更高，因此我們預測為正值。

最小二乘估計量的性質不受解釋變數之一僅包括0或1兩個數值這一事實的影響——D被看做任何一個其他解釋變數。我們能建立的一個區間估計值，或檢驗其最小二乘估計值的顯著性。這種檢驗就是地點對房價的影響是否“在統計上顯著”的統計檢驗。如果，則不存在所討論的位置溢價。

選擇參照組

取值D=0O和D=1的方便性能通過公式(4)看出。D=0定義了參照組或基準組，表示不在理想地區的房屋。這些房屋的預期價格僅為。運用公式(3)，我們來比較位於理想地區的房價和參照組的房價。

以解釋為目的，研究者選擇任何一個地區作為參照組都是最方便的。例如，我們能定義指示變數LD來表示非理想地區：

這個指示變數的定義正好與D相反，LD =1-D。如果將LD加入模型設定中：

則我們得到參照組，LD =0，表示房屋在理想地區。

你可能想在回歸模型中同時包括變數D和變數LD，以捕捉每種房屋地點對房價的影響。也就是說，你可能考慮如下模型：

在這個模型中，變數D和變數LD的關係是D+LD =1。由於截距變數，我們創造了一個具有完全共線性的模型，最小二乘估計量不適用於這些情況。這種錯誤有時被描述為陷入虛擬變數陷阱。通過只引入其中的一個指示變數，D或者LD，被省略的變數作為參照組，我們就避免了這個問題（避免虛擬變數陷阱的另一個方法是在模型中省略截距）。

斜率指示變數

假設地點對房價的影響不會導致特徵價格回歸方程(1)的截距發生變化，而是導致該關係式的斜率發生變化。通過在模型中引入一個等於指示變數和連續變數乘積的解釋變數，我們能描述斜率的變化。在該模型中，關係式的斜率代表新增1平方英尺的居住面積的價值。假設在理想地區和非理想地區這樣的價值不同，我們將回歸模型設定為：

新變數(SQFT×D)是房屋大小和指示變數的乘積，它被稱為互動變數，因為它表示地點和房屋大小對房價的互動作用效應。或者，它被稱為斜率指示變數或斜率虛擬變數，因為它考慮了關係式的斜率變化。當D=1時，對於位於理想地區的房屋，斜率指示變數的值等於SQFT；對於位於其他地區的房屋，其值等於零。儘管它有不同於普通變數的性質，在回歸模型中，斜率指示變數與其他解釋變數被同等對待。檢查兩個不同地區的回歸函式能最好地說明把斜率指示變數加入經濟模型的影響，

在理想地區，房屋每增加1平方英尺的價格是()，在其他地區是。如果在兩個地區中，更理想的地區每增加1平方英尺的價格更高，則我們預測。這種情況如圖2a所示。

另外一個觀測引入斜率指示變數的影響的方法是運用微積分。預期房價對房屋的大小（以平方英尺為衡量單位）求偏微分，得到關係式的斜率：

如果公式(5)滿足回歸模型的基本假設，其最小二乘估計量具有通常的良好性質。兩個地區新增1平方英尺的居住面積帶來的價值是否相等能通過假設檢驗來檢驗。在該檢驗中，原假設為，備擇假設為。在這種情況下，我們能檢驗對，因為我們預測影響效應是正的。

如果我們假設房屋位置同時影響截距和斜率，則這兩種影響能同時被引入一個模型中。得到的回歸模型為：

在本例中，兩個地區的房價回歸函式是：

在圖2b中，我們假設和，描述房價關係。

圖2(a)斜率指示變數

圖2(b)斜率和截距指示變數