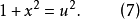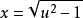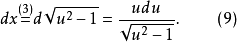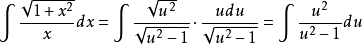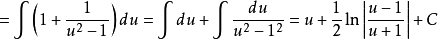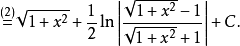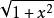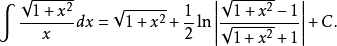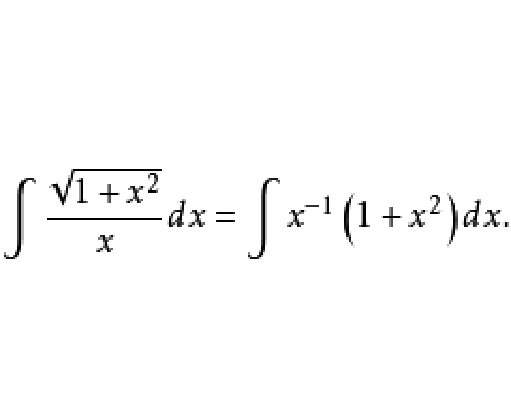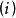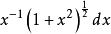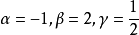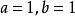二項微分式

形如x^α(a+bx^β)^γdx的表達式稱為“二項微分式”，其中a和b是實數；α，β，γ是有理數；x是自變數。

基本介紹

• 中文名：二項微分式
• 隸屬：微積分學
• 公式：x^p (a+b x^q)^r dx
• 確認者：牛頓

基本介紹

形如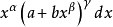 的表達式稱為“二項微分式”，其中 和b是實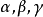數； 是有理數； 是自變數。

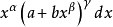
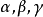
二項微分式的積分是初等函式的條件

設

為了給出F(x)為初等函式的條件，特作如下變換：令

則由(1)式得：

於是

把(2)，(3)兩式代人 式，得：

(4)式右邊表示的仍是二項微分式的積分，不過此時的積分變數是t，它的積分結果是t的函式。為了討論的方便，不妨把這個函式記為 ，即

只要

這三個數中有一個是整數，則二項微分式的積分(5)的結果就一定是初等函式。

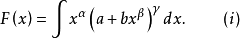
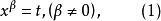
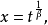
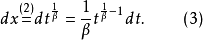
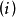
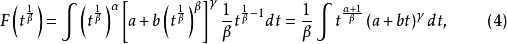
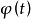
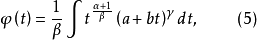
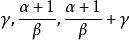
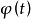
二項微分式的積分方法

契貝謝夫法

定理1 契貝謝夫(1821-1894，俄國數學家)定理 在二項微分式的積分：

中，(1)當 為整數時，可令 (其中N是有理數 的公分母)；

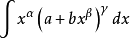
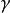
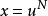
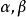
(2)當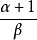 為整數時，可令 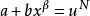(其中N是有理數 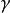的分母)；

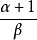
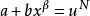
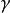
(3)當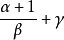 是整數時。可令 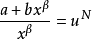(其中N是有理數 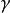的分母)。

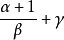
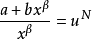
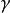
舉例分析

下面舉例，以具體地說明如何利用上述定理求二項微分式的積分。

例1 求不定積分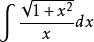

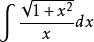
解：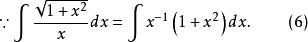

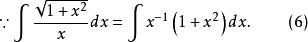
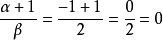
將(6)式右邊與公式相比照，不難看出，所給積分是二項微分式的積分，在這裡(有理數)，，並且

(整數)．

根據定理1中所講的方法(第2種情形)，需令：

由（2）式得：

(取). (8)

把(2)，(3)，(4)式代入(1)式，得：

(根據(2)式把還原成)，即