二進制

二進制（binary）在數學和數字電路中指以2為基數的記數系統，以2為基數代表系統是二進位制的。這一系統中，通常用兩個不同的符號0（代表零）和1（代表一）來表示。數字電子電路中，邏輯門的實現直接套用了二進制，因此現代的計算機和依賴計算機的設備里都用到二進制。每個數字稱為一個比特（Bit，Binary digit的縮寫）。

基本介紹

• 中文名：二進制
• 外文名：binary system
• 類別：算法
• 屬性：計數法

計數系統

在基數b的位置記數系統(其中b是一個正自然數，叫做基數)，b個基本符號(或者叫數字)對應於包括0的最小b個自然數。 要產生其他的數，符號在數中的位置要被用到。最後一位的符號用它本身的值，向左一位其值乘以b。一般來講，若b是基底，我們在b進制系統中的數表示為 的形式，並按次序寫下數字a₀a₁a₂a₃...a_k。這些數字是0到b-1的自然數。

一般來講，b進制系統中的數有如下形式：

數 和 是相應數字的比重。

二進制

17世紀至18世紀的德國數學家萊布尼茨，是世界上第一個提出二進制記數法的人。用二進制記數，只用0和1兩個符號，無需其他符號。

二進制數據也是採用位置計數法，其位權是以2為底的冪。例如二進制數據110.11，逢2進1，其權的大小順序為2²、2¹、2º、 、 。對於有n位整數，m位小數的二進制數據用加權係數展開式表示，可寫為：

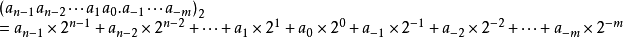
二進制數據一般可寫為：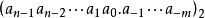

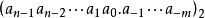
【例】：將二進制數據111.01寫成加權係數的形式。

解：

二進制和十六進制，八進制一樣，都以二的冪來進位的。

運算

加法

二進制加法有四種情況： 0+0=0，0+1=1，1+0=1，1+1=10(0 進位為1)。

乘法

二進制乘法有四種情況： 0×0=0，1×0=0，0×1=0，1×1=1。

減法

二進制減法有四種情況：0－0=0，1－0=1，1－1=0，0－1=1。

除法

二進制除法有兩種情況(除數只能為1)：0÷1=0，1÷1=1。

實例

兩個二進制數1001與0101的算數運算可表示為：

1001與0101的算術運算

進制轉換

二進制轉換為十進制

方法：“按權展開求和”，該方法的具體步驟是先將二迸制的數寫成加權係數展開式，而後根據十進制的加法規則進行求和。

【例】：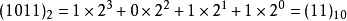

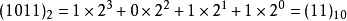
規律：個位上的數字的次數是0，十位上的數字的次數是1，......，依次遞增，而十分位的數字的次數是-1，百分位上數字的次數是-2，......，依次遞減。

十進制轉換為二進制

一個十進制數轉換為二進制數要分整數部分和小數部分分別轉換，最後再組合到一起。

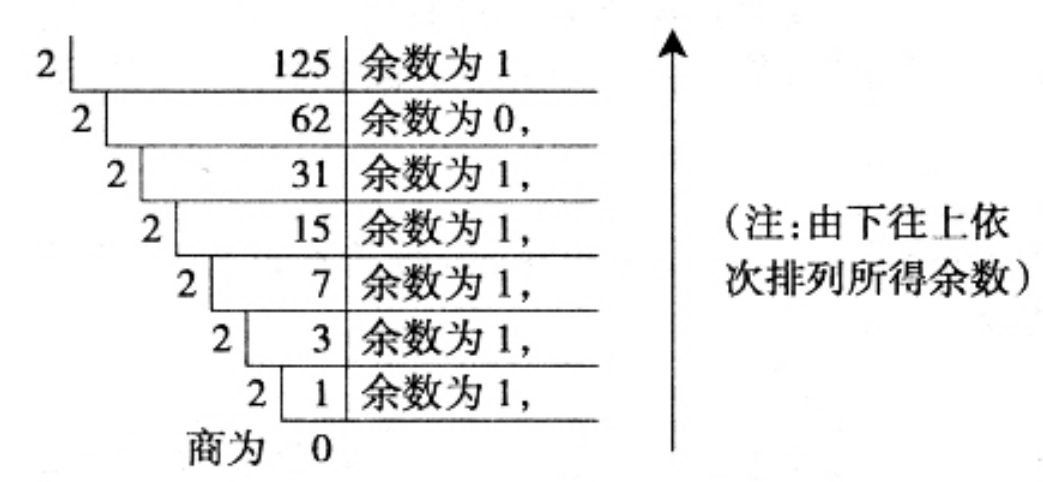整數部分採用 "除2取余，逆序排列"法。具體做法是：用2整除十進制整數，可以得到一個商和餘數；再用2去除商，又會得到一個商和餘數，如此進行，直到商為小於1時為止，然後把先得到的餘數作為二進制數的低位有效位，後得到的餘數作為二進制數的高位有效位，依次排列起來。例：125。

整數部分

小數部分要使用“乘 2 取整法”。即用十進制的小數乘以 2 並取走結果的整數(必是 0 或 1)，然後再用剩下的小數重複剛才的步驟，直到剩餘的小數為 0 時停止，最後將每次得到的整數部分按先後順序從左到右排列即得到所對應二進制小數。例如，將十進制小數 0.6875 轉換成二進制小數過程如下:

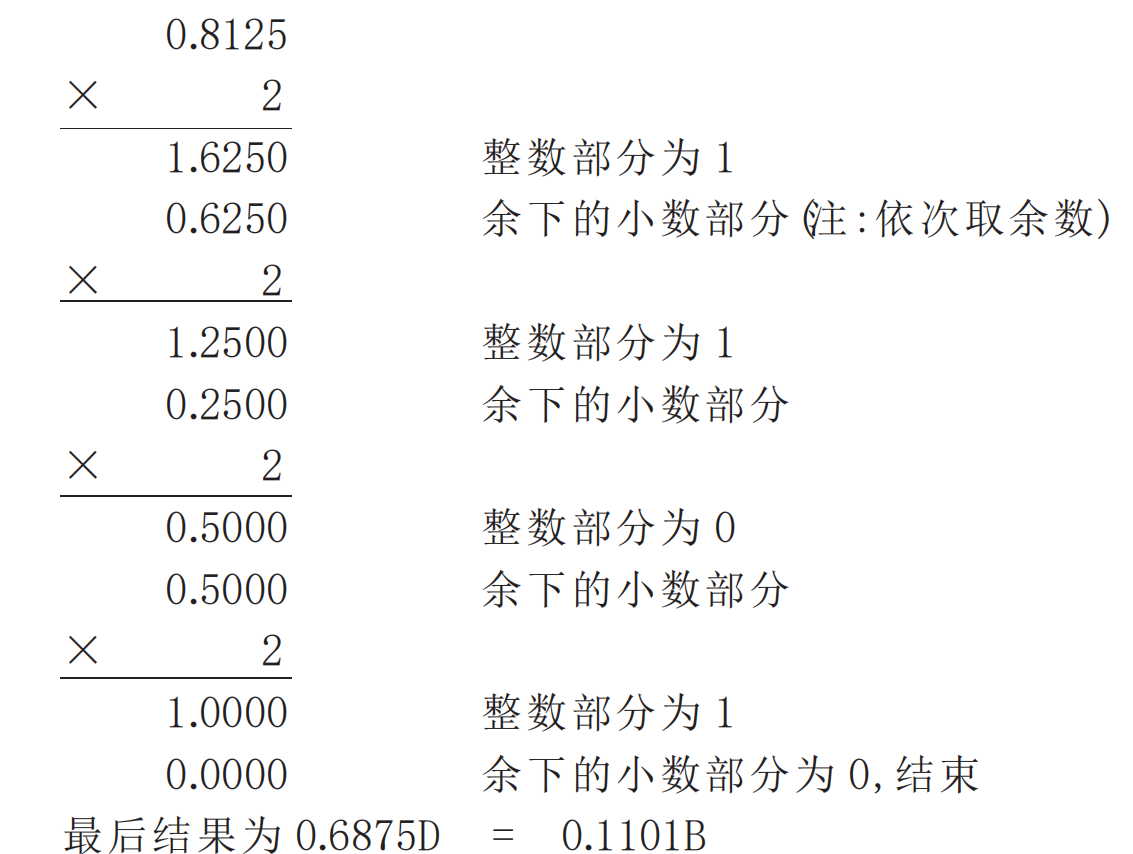小數部分

通用進制轉換

不同進制之間的轉換本質就是確定各個不同權值位置上的數碼。轉換正整數的進制的有一個簡單算法，就是通過用目標基數作長除法；餘數給出從最低位開始的“數字”。例如，1020304從10進制轉到7進制：

十進制轉換為七進制

再如，10110111 從2進制到5進制：

二進制轉換為五進制

計算機採用二進制原因

首先，二進位計數制僅用兩個數碼。0和1，所以，任何具有二個不同穩定狀態的元件都可用來表示數的某一位。而在實際上具有兩種明顯穩定狀態的元件很多。例如，氖燈的"亮"和"熄"；開關的”開“和”關“; 電壓的”高“和”低“、”正“和”負“；紙帶上的”有孔“和“無孔”，電路中的”有信號“和”無信號“, 磁性材料的南極和北極等等，不勝枚舉。 利用這些截然不同的狀態來代表數字，是很容易實現的。不僅如此，更重要的是兩種截然不同的狀態不單有量上的差別，而且是有質上的不同。這樣就能大大提高機器的抗干擾能力，提高可靠性。而要找出一個能表示多於二種狀態而且簡單可靠的器件，就困難得多了。

其次，二進位計數制的四則運算規則十分簡單。而且四則運算最後都可歸結為加法運算和移位，這樣，電子計算機中的運算器線路也變得十分簡單了。不僅如此，線路簡化了，速度也就可以提高。這也是十進位計數制所不能相比的。

第三，在電子計算機中採用二進制表示數可以節省設備。可 以從理論上證明，用三進位制最省設備，其次就是二進位制。但由於二進位制有包括三進位制在內的其他進位制所沒有的優點，所以大多數電子計算機還是採用二進制。此外，由於二進制中只用二個符號 “ 0” 和“1”，因而可用布爾代數來分析和綜合機器中的邏輯線路。 這為設計電子計算機線路提供了一個很有用的工具。