基本介紹
- 中文名：二次組態相互作用
- 學科：計算機
簡介,組態相互作用方法,大小一致性問題,
簡介
組態相互作用方法
組態相互作用方法(CI) 是一種後Hartree-Fock方法，求解的是多電子體系在波恩-奧本海默近似下的非相對論薛丁格方程。“構型相關”有兩層含義：“構型" 從數學角度簡潔的表述了它是描述波函的斯雷特行列式的線性耦合。根據軌道占據的規則 (例如, (1s)(2s)(2p)...)，“相關”的意思是不同電子構型（態）之間的混合（相互作用）。由於CI計算的CPU計算時間很長以及需要巨大的硬體資源，所以這個方法只能用於相對較小的體系。
與Hartree-Fock方法相比，為了計入電子相關作用，CI方法使用了由組態態函式（CSF）線性耦合得到的變分波函式，而這些組態態函式是由自旋軌道（用上標SO表示）構建的。
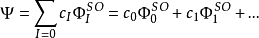
在這裡， Ψ通常是指體系的電子基態。如果展開項包括了合適對稱性的所有可能的 CSF, 則就是完全組態相互作用，它可以準確的求解由單粒子基組限定的空間內的電子薛丁格方程。上述展開項中的第一個就是Hartree-Fock行列式. 其他的構型態函式可以通過虛軌道和Hartree-Fock行列式中的自旋軌道交換的數目來表征。如果僅有一個自旋軌道不一樣，我們就稱它為單激發行列式。如果有兩個自旋軌道不一樣，就是雙激發行列式，其餘的以此類推。例如，CID方法只包含雙重激發項，CISD方法包含單激發和雙激發項。單激發項不和Hartree-Fock行列式混合。很多標準的程式中都有CID和CISD方法。戴維森校正可以被用於評估相對於CISD能量的矯正以說明更高的激發。求解CI方程的同時，也得到近似的激發態，這些激發態的係數cI是不一樣的。
大小一致性問題
量子化學中的大小一致性或嚴格可分離性是保證無相互作用的體系（如距離無限遠）能量計算一致的一種性質。這種性質往往是針對某種方法而言的。
如果A和B是兩個無相互作用的體系。如果某方法是大小一致的，那么該方法得到的體系 A-B 的能量等於體系 A 的能量計算結果與體系 B 的能量計算結果之和。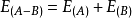
。在處理解離曲線等問題時，這個性質尤其重要。
