歷史發展,起源,近代發展,組成元素,解題手法,基礎解法,進階解法,區塊摒除法,數對法,其他進階解法介紹,高級技巧,難度劃分,終盤數量,標準數獨,變形數獨,對角線數獨,迷你數獨,鋸齒數獨,連體數獨,Killer數獨,出題方法,挖洞法,填數法,類似謎題,數獨軟體,數獨賽事,
歷史發展
起源
既然“數獨”有一個字是“數”,人們也往往會聯想到數學,那就不妨從大家都知道的數學家
歐拉說起,但凡想了解數獨歷史的玩家在網路、書籍中搜尋時,共同會提到的就是歐拉的“拉丁方塊(Latin square)”。
拉丁方塊的規則:每一行(Row)、每一列(Column)均含1-N(N即盤面的規格),不重複。這與前面提到的標準數獨非常相似,但少了一個宮的規則。
近代發展
數獨起源於18世紀初瑞士數學家
歐拉等人研究的
拉丁方陣(Latin Square)。19世紀80年代,一位美國的退休建築師格昂斯(Howard Garns)根據這種拉丁方陣發明了一種填數趣味遊戲,這就是數獨的雛形。20世紀70年代,人們在美國紐約的一本益智雜誌《Math Puzzles and Logic Problems》上發現了這個遊戲,當時被稱為填數字(Number Place),這也是公認的數獨最早的見報版本。1984年一位日本學者將其介紹到了日本,發表在Nikoli公司的一本遊戲雜誌上,當時起名為“數字は獨身に限る”(すうじはどくしんにかぎる),就改名為“數獨”(すうどく),其中“數”(すう)是數字的意思,“獨”(どく)是唯一的意思。後來一位前任
香港高等法院的紐西蘭籍法官高樂德(Wayne Gould)在1997年3月到日本東京旅遊時,無意中發現了。他首先在英國的《
泰晤士報》上發表,不久其他報紙也發表,很快便風靡全英國,之後他用了6年時間編寫了電腦程式,並將它放在網站上(這個網站也就是著名的數獨玩家論壇),後來因一些原因,網站被關閉,幸好
數獨大師Glenn Fowler恢復了數據,玩家論壇有了新處所。在90年代國內就有部分的益智類書籍開始刊登,南海出版社在2005年出版了《數獨1-2》,隨後日本著名數獨制題人西尾徹也的《
數獨挑戰》也由
遼寧教育出版社出版。《
北京晚報》、《
揚子晚報》、《
羊城晚報》、《
新民晚報》、《
成都商報》等等報紙媒體也先後刊登了數獨遊戲。
組成元素
方格
水平方向有九橫行,垂直方向有九縱列的矩形,畫分八十一個小
正方形,稱為
九宮格(Grid),如圖一所示,是數獨(Sudoku)的作用範圍。
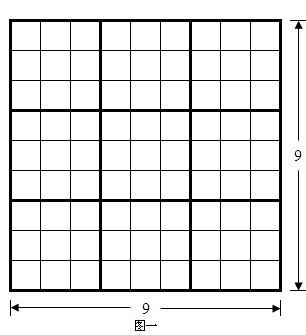 數獨元素 - 九宮格
數獨元素 - 九宮格行
水平方向的每一橫行有九格,每一橫行稱為行(Row),如圖二所示。
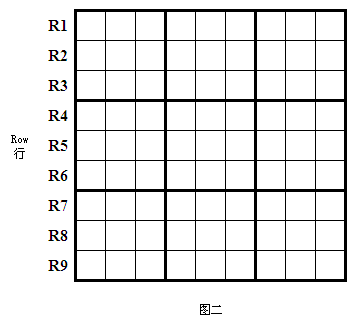 數獨元素 - 單元
數獨元素 - 單元列
垂直方向的每一縱列有九格,每一縱列稱為列(Column),如圖三所示。
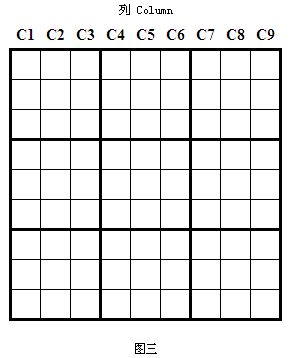 數獨元素 - 列
數獨元素 - 列宮
三行與三列相交之處有九格,每一單元稱為小九宮(Box、Block),簡稱
宮,如圖四所示(在殺手數獨中,宮往往用單詞Nonet表示)。
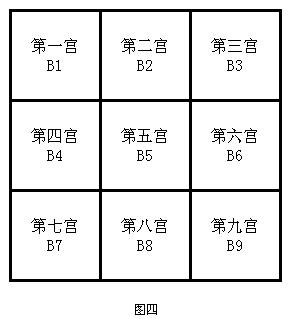 數獨元素 - 宮
數獨元素 - 宮組成
上述行、列、宮、單元格統稱為單元(Unit);而行、列、宮統稱為區域(Region)。
區塊
由三個連續宮組成大行列(Chute),分大行(Floor)及大列(Tower)。
第一大行:由第一宮、第二宮、第三宮組成。
第二大行:由第四宮、第五宮、第六宮組成。
第三大行:由第七宮、第八宮、第九宮組成。
第一大列:由第一宮、第四宮、第七宮組成。
第二大列:由第二宮、第五宮、第八宮組成。
第三大列:由第三宮、第六宮、第九宮組成。
格位編號
格位按所處的行列單元賦予坐標值,如圖五所示。
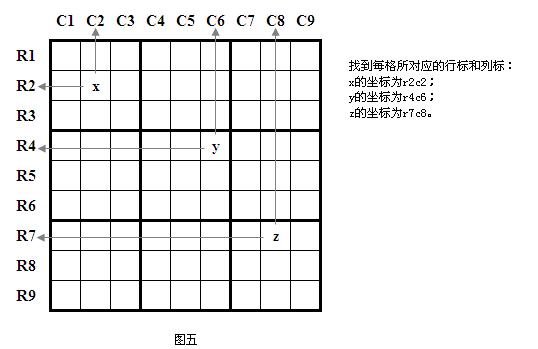 數獨元素 - 格位
數獨元素 - 格位坐標有多種標示法,有橫行 A~I,縱列 1~9(如中國),也有橫行 1~9,縱列 A~I(如日本),這兩種標示容易混淆,故最被廣泛使用的是橫行R1~R9,縱列C1~C9的標示法。
提示數
在九宮格的格位填上一些數字,做為填數判斷的
線索(Hint),稱為提示數(Clue),如圖六所示。
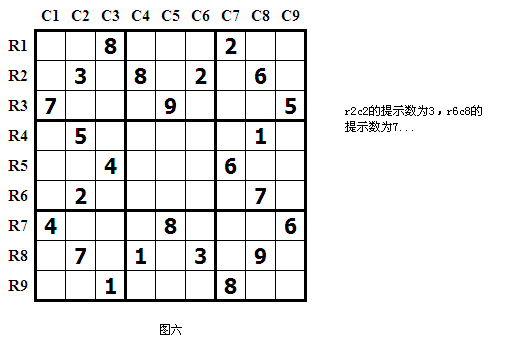 數獨元素 - 提示數
數獨元素 - 提示數解題手法
依解題填制的過程可區分為直觀法與候選數法。
直觀法就是不做任何記號,直接從數獨的盤勢觀察線索,推論答案的方法。
候選數法就是刪減等位群格位已出現的數字,將剩餘可填數字填入空格做為解題線索的參考,可填數字稱為候選數(Candidates,或稱備選數)。
直觀法和候選數法只是填制時候是否有註記的區別,依照個人習慣而定,並非鑑定題目難度或技巧難度的標準,無論是難題或是簡單題都可上述方法填制,一般程式解題以候選數法較多。
基礎解法
排除法(摒除法)
摒除法:用數字去找單元內唯一可填空格,稱為摒除法,數字可填唯一空格稱為排除法 (Hidden Single)。
根據不同的作用範圍,摒余解可分為下述三種:
數字可填唯一空格在「宮」單元稱為宮排除(Hidden Single in Box),也稱宮摒除法。
數字可填唯一空格在「行」單元稱為行排除法(Hidden Single in Row),也稱行摒除法。
數字可填唯一空格在「列」單元稱為列排除法(Hidden Single in Column),也稱列摒除法。
唯一餘數法
唯一餘數法:用格位去找唯一可填數字,稱為餘數法,格位唯一可填數字稱為唯余解(Naked Single)。
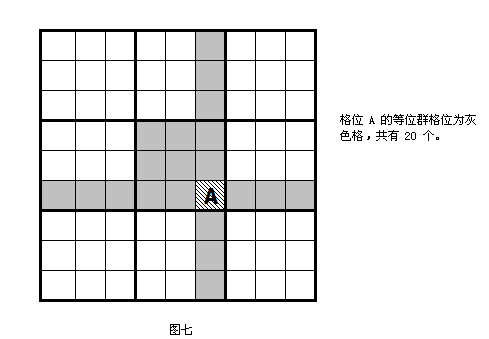 Peer等位群格位
Peer等位群格位餘數法是刪減等位群格位(Peer)已出現的數字的方法,每一格位的等位群格位有 20 個,如圖七所示。
進階解法
上述方法稱為基礎解法(Basic Techniques),其他所有的解法稱為進階解法(Advanced Techniques),是在補基本解法之不足,所以又稱輔助解法。
進階解法包括:區塊摒除法(Locked Candidates)、數組(Subset/Tuple)、二鏈列(X-Wing)、唯一矩形(Unique Rectangle)、全雙值格致死解法(Bivalue Universal Grave)、同數鏈(X-Chain)、異數鏈(Multidigit Chain)及其他數鏈的高級技巧等等。已發展出來的方法有近百種之多。
其中前三種加上基礎解法為一般數獨書中介紹並使用的方法,同時也是大部分人可以理解並掌握的數獨解題技法。
通過基礎解法出數只需一種解法,摒除法或唯余法,超出此範圍而需要施加進階解法時,解題點需要進階解法協助基礎解法來滿足隱性唯一或顯性唯一才能出數,該解題點的解法需要多個步驟協力完成,因此稱做組合解法。
解題必須以邏輯為依歸,提倡數獨的本意。
區塊摒除法
區塊摒除法包括宮區塊摒除法(Pointing)與行列區塊摒除法(Claiming)。
在基礎題里,利用區塊摒除可以替代一些基礎解法的觀察,或輔助基礎解法尋找焦點。
在非基礎題里,區塊可以隱藏任何其他結構,簡單的可以把基礎解法隱藏起來,難的可以隱藏數對等等其他進階技巧。
例如:
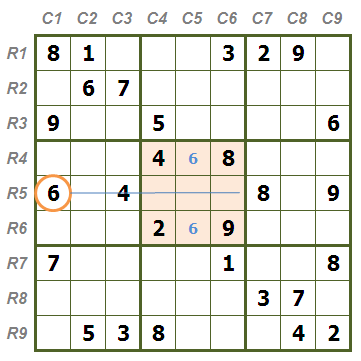 區塊摒除法
區塊摒除法首先數字6對第五宮摒除,得到第五宮的6在R4C5或者R6C5。
不論是在R4C5或者R6C5,C5的其他格都不能再有數字6。(R4C5與R6C5就是數字6的區塊,這也是區塊摒除作用的觀點)
數字6對第二宮摒除,得解R1C4=6。
數對法
當一個單元(行、列、宮)的某兩個數字僅可能在某兩格時,我們稱這兩個格為這兩個數的數對(Pairs)。
數對出現在宮稱為宮數對;數對出現在行列成為行列數對。
用候選數法的觀點去看,數對有兩種,一種是在同單元內其中兩格有相同的雙候選數,一看就明白,因此稱為顯性數對(Naked Pair),另一種是,同單元內有兩個候選數占用了相同的兩格,該兩格因為還有其它候選數很難辨認,因此稱為隱性數對(Hidden Pair)。
例子:
左圖:數字2與7同時對第一宮摒除,得到這兩個數字均只可能在r2c2與r3c2這兩個位置,我們稱r2c2與r3c2是27數對。
右圖:數字8對第一宮摒除,得到摒余解r1c3=8。
其他進階解法介紹
三鏈數/Triplet
四鏈數/Quad
全雙值墳墓(Bivalue Universal Grave)
Unique Rectangle type 1
Unique Rectangle type 2
Unique Rectangle type 3
Unique Rectangle type 4
Unique Loop
高級技巧
入門:強弱鏈的定義及關係(Strong Link & Weak Link)
四角對角線法則/矩形刪除法(X-Wing)
摩天樓(Skyscraper)
雙線風箏(Two Strings Kite)
多寶魚(Fish/Turbot)
X鏈/X-Chain
X環/X-Cycle
守護者(Guardians)
三鏈列/Swordfish
四鏈列/Jellyfish
Finned X-Wing
Group X-Chain
Empty Rectangle(空矩形)
Finned Swordfish
Fish
XY-Wing
XY-Chain
Multi X-Wing/XY-Cycle
遠程數對(Remote Pairs)
欠一數對(Almost Locked Pair)
Y-Wing/W-Wing
XYZ-Wing
M-Wing
Sue de coq/ALS(Almost Locked Subset)
Double Loop
Hidden Unique Rectangle
Unique Rectangle 6-cell
難度劃分
影響數獨難度的因素很多,就題目本身而言,包括最高難度的技巧、各種技巧所用次數、是否有隱藏及隱藏的深度及廣度的技巧組合、當前盤面可邏輯推導出的出數個數等等。對於玩家而言,了解的技巧數量、熟練程度、觀察力自然也影響對一道題的難度判斷。市面上數獨刊物良莠不齊,在書籍、報紙、雜誌中所列的難度或者大眾解題時間純屬參考,常有難度錯置的情況出現,所以不必特別在意。網路上有很多數獨難度的分析軟體,比較著名的是 Nicolas Juillerat 開發的 Sudoku Explainer 和 Bernhard Hobiger 開發的 Hodoku,它們都是免費的軟體。因為每種軟體的都有不同的解題策略,所以也只能作為難度的大致界定,無法真正的解析出難度的內涵。
如果一道題目的提示數少,那么題目就會相對難,提示數多則會簡單,這是一般人判斷難易的思維模式,但數獨謎題提示數的多寡與難易並無絕對關係,多提示數比少提示數難的情況屢見不鮮,同時也存在增加提示數之後題目反而變難的情形,即使是相同提示數(甚或相同謎題圖形)也可以變化出各式各樣的難度。提示數少對於出題的困難度則有比較直接的關係,以20-35提示數而言,每少一個提示數,其出題難度會增加數倍,在製作謎題時,提示數在22以下就非常困難,所以常見的數獨題其提示數在23~30之間,其原因在於製作比較不困難,可以設計出比較漂亮的圖形(Pattern),另外這個提示數範圍的謎題變化多端是一個重要因素。
終盤數量
數獨中的數字排列千變萬化,那么究竟有多少種終盤的數字組合呢?
6,670,903,752,021,072,936,960(約為6.67×10的21次方)種組合,2005年由Bertram Felgenhauer和Frazer Jarvis計算出該數字,並將計算方法發布在他們網站上,如果將等價終盤(如旋轉、翻轉、行行對換,數字對換等變形)不計算,則有5,472,730,538個組合。數獨終盤的組合數量都如此驚人,那么數獨題目數量就更加不計其數了,因為每個數獨終盤又可以製作出無數道合格的數獨題目。
標準數獨
目前(截止2011年)發現的最少提示數9×9
標準數獨為17個提示,截止2011年11月24日16:14,共發現了非等價17提示數謎題49151題,此數量仍在緩慢上升中,如果你先發現了17提示數的題目,可以上傳至“17格數獨驗證”網站,當然你也可以在這裡下載這49151題。
關於是否有16提示數的合格題目,網路上也爭論很久,有發現16提示數雙解的,但是仍未發現唯一解。國外有網友給出了關於為什麼至少需要17提示的證明,受到了大家的質疑,比如9×9
對角線數獨(在標準數獨規則基礎上,兩條大對角線的數字不重複)的最小提示數為12,按照他的理論則需要更多的提示數。
另外在2006年Gary McGuire撰寫了程式,試圖通過暴力法來證明16提示數的數獨是否存在,方法很簡單,既然Bertram Felgenhauer和Frazer Jarvis已經計算出不等價的終盤總數為5,472,730,538個,那么將每個終盤是16提示的情況都跑一遍,如果沒有找到16提示的數獨,那么就可以證明最少提示數為17個。但因為是暴力方法,對於一台單核的電腦來說需要跑30萬年才能跑出結果。台灣的吳毅成教授和他的團隊將Gary McGuire的程式加以改進,使得效率大幅提升,大約2417年即可完成演算。並放在
BOINC(伯克利開放式網路計算平台)上讓世界加入BOINC的電腦一同演算,令人欣喜的是,截至編輯2012年4月18日已經完成了51.73%。
Gary McGuire的團隊在2009年設計了新的算法,利用致命結構的思路,花費710萬小時CPU時間後,於2012年1月1日提出了9×9標準數獨不存在16提示唯一解的證明,繼而說明最少需要17個提示數。並將他們的論文以及原始碼更新在2009年的頁面上。
變形數獨
數獨到如今發展,出現了越來越多的
變形(Variants),按照規則劃分則成百上千,各國的數獨愛好者也不斷製作出新的變形。
一般意義上,按照最為基礎的數獨規則,一般稱為標準數獨(Standard Sudoku)。而產生的解題思路和技巧,也稱為
標準數獨技巧。
下面列出最常見的幾種變形:
對角線數獨
對角線數獨(Diagonal Sudoku、Sudoku-X):
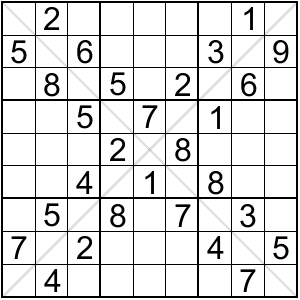 對角線數獨
對角線數獨迷你數獨
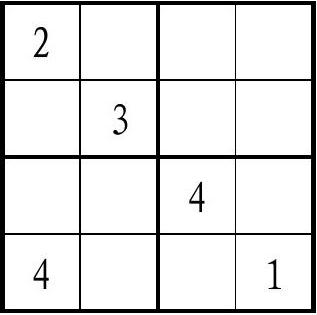
迷你數獨(Mini Sudoku):
每個謎題都由一個在不同位置給與提示數字的4x4或6x6格線組成。遊戲的目的是將空方格填上數字1到4(對於4x4大小的謎題)或者1到6(對於6x6的謎題),使得每一行,每一列以及每一個宮都沒有重複的數字出現。
鋸齒數獨
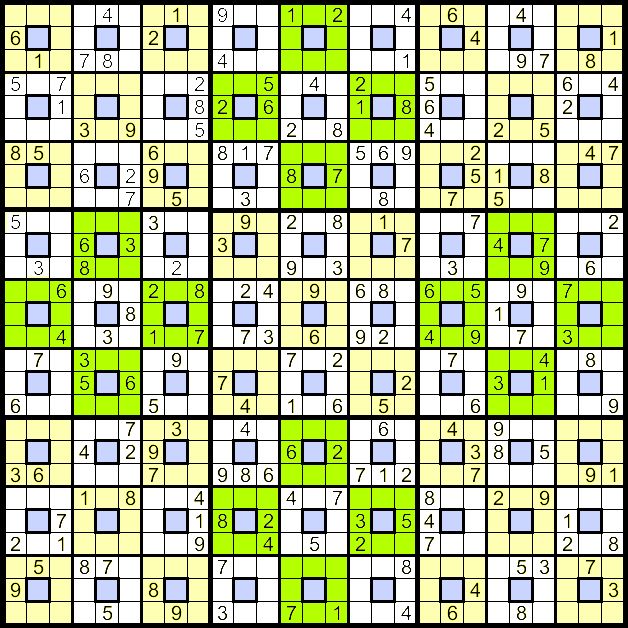
鋸齒數獨(Jigsaw Sudoku):
相對標準數獨而言,宮變成了不規則的。玩家需在對應的鋸齒方框內填入不重複的九個數或N個數,並保證橫縱也不重複。
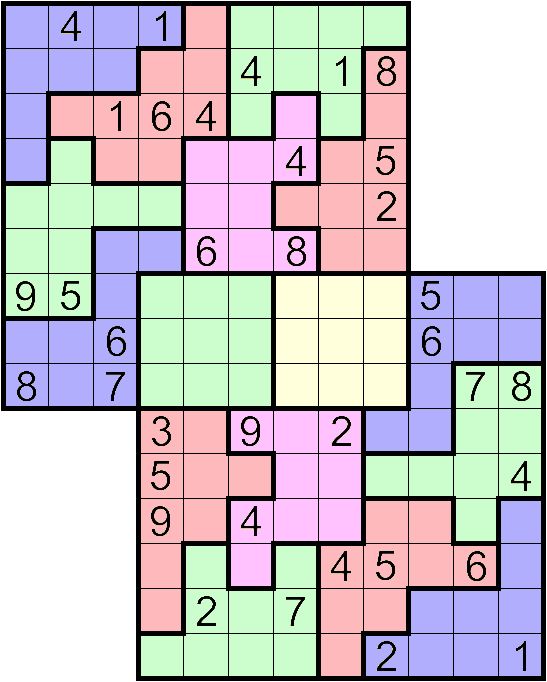
連體數獨
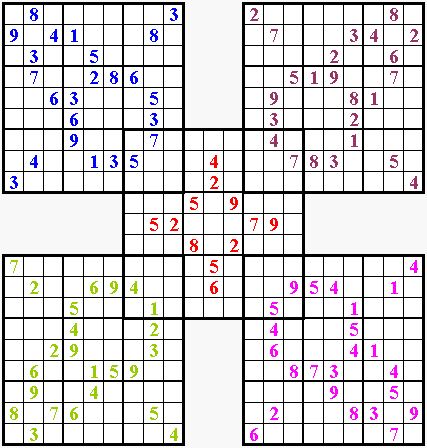
連體數獨(Multi Sudoku):
每個謎題都由倆個或者更多的數獨格線重疊組成,該格線可能是標準數獨謎題也可能是混合類型的數獨謎題,這些格線都有一個或多個宮重疊。遊戲的目的是通過其規則將每個格線均解出。溫馨提示,重疊的區域必須同時滿足其所在格線的規則。
Killer數獨
殺手數獨(Killer Sudoku、Sum Sudoku):
在標準數獨規則的基礎上,每個虛線框左上角的數字表示虛線框內所有數字之和,每個虛線框內數字無重複。
 殺手數獨
殺手數獨對角線數獨引發了額外區域等,鋸齒數獨打破了宮是方方正正的定式,殺手數獨更是引發了更多計算類的數獨。
出題方法
挖洞法
從有到無的出題方法。先生成一個終盤,然後挖去部分數字形成一道題目。
填數法
從無到有的出題方法。在一個空盤面上填上部分數字形成一道題目。值得一提的是,2007年日本NPGenerator軟體的網站提出了一種邊推理邊出題的出題法,可以手工打造出漂亮圖案的數獨題目,有興趣出題的可以試試。
類似謎題
謎題(Puzzle):排除文化差異對做題者的影響,只用數字和圖形表示的邏輯推理遊戲。數獨是謎題中的一個成員,由於其規則簡單、種類眾多從而從眾多謎題脫穎而出,成為大眾熟知的數字謎題。
不過除了數獨以外,還有不少謎題也非常出色,也有眾多的擁護者,而且與數獨有千絲萬縷的關係。數獨愛好者同樣不能錯過這些優秀的邏輯推理遊戲。下面簡單介紹幾類謎題:
數和(Kakuro):與殺手數獨很像的一類謎題,規則要求同行、同列(同一段)數字不能重複,且每段數字之和等於左邊和上邊的提示數字。
數圖(Nonograms/Griddlers):根據盤面周圍的數字提示,把盤中塗成符合條件的圖案,很像“十字繡”。
數回(Slither Link):遊戲由0,1,2,3四個數字組成。每一個數字,代表四周劃線的數目,並在最後成為一個不間斷、不分岔的迴路。
數牆(Nurikabe):數牆的世界,是一個非黑即白的二元世界;在遊戲中,你要決定的是,哪些格子需要塗黑,哪一些應該留白。
數連(Number Link):與數獨一樣,數連是一個簡單明快的遊戲。你只需要把屬於相同數字的同伴,以線連線起來。不過,這個遊戲看起來非常簡單,實際上是很有深度的。
算獨(Kenken)遊戲的目的是將數字1到N(N為格線的行列數)填滿空格,使得每一行,每一列的數字不重複,並且每一個粗線框左上角代表了該粗線框內數字的運算法則以及計算結果。算數數獨的粗線框內,相同數字可能使用不止一次。
數獨軟體
數獨軟體現在比較多,影響比較大,功能比較全的有以下軟體:
hodoku,Sudoku Explainer,SudoCue,Simple Sudoku,Color Sudoku,無限數獨等。
一個好的數獨軟體應當可以進行一步一步計算、指定步數計算、一次性計算,對於每一步計算給出詳細的說明。對於有多個解的數獨題目,會給出提示,並可人工干預。對每一步計算生成步驟列表,可以回到任意步驟進行研究。
【hodoku】,用於分析標準數獨難度及產生標準數獨題目。功能相當強大。免費下載,提供了超詳細的解題過程分析。
【Sudoku Explainer】,用於分析標準數獨難度及產生標準數獨題目。本軟體的難度分析評分極具權威性。
【SudoCue】,功能強大,免費。還可以生成多種變形數獨。
【Simple Sudoku】,功能強大,免費。
【Color Sudoku】,用於生成標準數獨、對角線數獨、killer數獨、GT數獨(跨宮標)、連續數獨、連體數獨及上述任意幾種規則的組合題型,可選擇提示數是否180度對稱,可批量列印上述題目。功能強大,免費。
無限數獨,是國人開發,免費,簡單易用。可惜作者原始碼丟失後不在繼續開發了。
數獨賽事
世界數獨錦標賽:由
世界智力謎題聯合會組織的國際性最高水準數獨賽事,該賽事每年舉辦一次,由不同的會員國輪流申請舉辦。首屆於2006年在義大利的盧卡舉辦,第八屆於2013年在北京舉辦。每年由世智聯在各國的唯一授權組織選拔國家隊參加。
北京國際數獨大獎賽:由
北京廣播電視台主辦的一項國際數獨賽事,該賽事獎金較高,也吸引了國際上眾多高手踴躍參與,給國內高手提供了一個可以與國外高手同場競技的平台。首屆於2011年舉辦,第二屆於2012年5月舉辦,目前國內參賽的選手均為以往進入過數獨國家隊或在國內選拔賽中名列前茅者。
中國數獨錦標賽:由國內的世智聯授權組織每年舉辦一次,目的是選拔出當年的數獨高手組隊參加一年一度的世界數獨錦標賽。該比賽不設定門檻,無論新人還是老手均可參加。具體的時間和地點請關注官方的數獨選拔賽通知。
經過兩天緊張激烈的比賽,各項桂冠終有歸屬。中國隊獲得團體賽冠軍,捷克、日本分獲亞軍、季軍;中國隊的三位中學生選手金策、孫徹然、邱言哲獲18歲及18歲以下年齡組前三名;中國隊梁躍獲得50歲及50歲以上年齡組亞軍,丹麥隊和義大利隊選手分獲冠軍和季軍;金策還奪得個人賽冠軍,日本的森西亨泰、捷克的雅庫布分獲亞軍、季軍。
據了解,隨著數獨這項智力運動在中國的不斷普及,越來越多的青少年成為數獨愛好者。此次中國數獨代表隊不僅是比賽中最年輕的國家隊之一,年僅15歲的邱言哲也成為年齡最小的A隊隊長。別看他還是一名在校國中生,卻有著豐富的比賽經驗,2011、2012年他曾是世界數獨錦標賽中國隊選手,2013獲得中國數獨錦標賽第四名。
獲得18歲及18歲以下年齡組、個人賽及團體賽三項冠軍的中學生金策,可謂本屆數獨世錦賽的一匹黑馬。來自浙江的他已與數獨結緣4年,當一些同齡人沉溺於網路遊戲時,他卻利用網路尋找與他志同道合的數獨夥伴。瘦高的個子,不善言語的他,雖然在陌生人面前有些羞澀,但卻通過一個個小小的九宮格展現自信與智慧。
本屆數獨世錦賽決賽以電視直播的方式,在北京電視台新聞頻道同步播出,這在世界上尚屬首次。在沒有任何經驗可循的情況下,為保證不影響賽事進行,同時又能實時展現選手比賽進程,組委會設計了多套直播方案,多次推敲併到場演練,以演播室講解加決賽現場的方式,清晰簡練地為電視觀眾講解數獨題目。
 數獨元素 - 九宮格
數獨元素 - 九宮格 數獨元素 - 單元
數獨元素 - 單元 數獨元素 - 列
數獨元素 - 列 數獨元素 - 宮
數獨元素 - 宮 數獨元素 - 格位
數獨元素 - 格位 數獨元素 - 提示數
數獨元素 - 提示數 Peer等位群格位
Peer等位群格位 區塊摒除法
區塊摒除法 對角線數獨
對角線數獨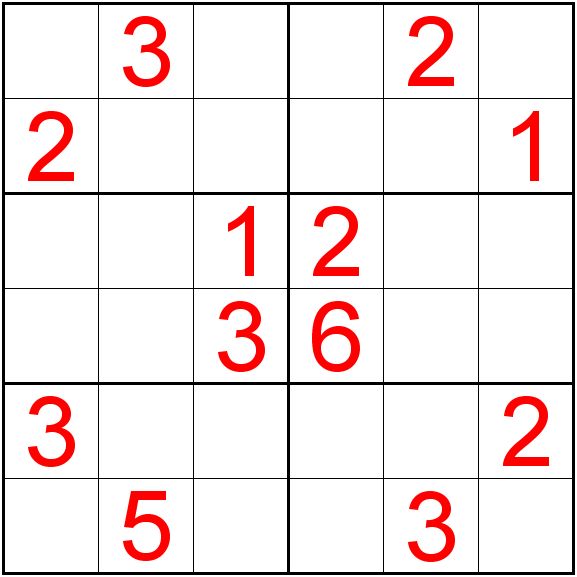

 殺手數獨
殺手數獨
