主分式理想群(group of principal fractionalideals)戴德金整環的全分式理想群的子群.設P(R)表示戴德金整環的一切非零主分式理想的集合。
定義
主分式理想群(group of principal fractionalideals)戴德金整環的全分式理想群的子群.設P(R)表示戴德金整環的一切非零主分式理想的集合，由分式理想的乘法知:
因此，P(R)做成一個交換群，稱為R的主分式理想群.
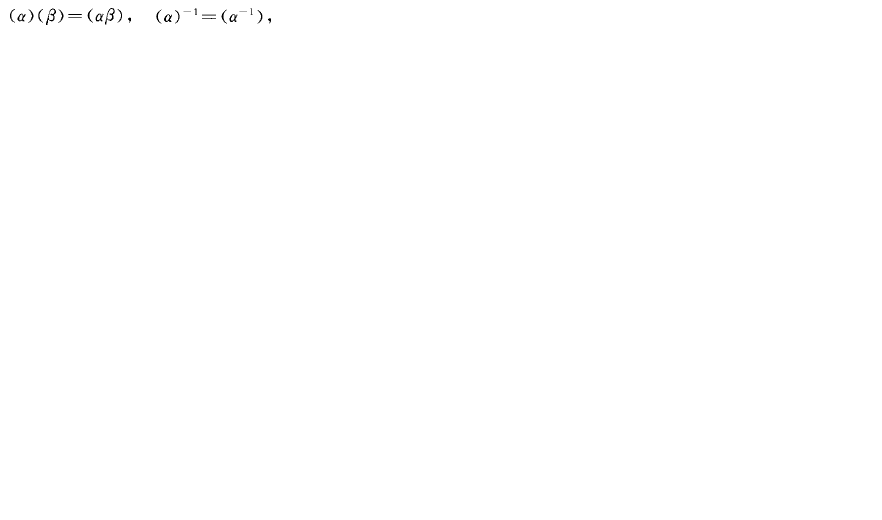
主分式理想群(group of principal fractionalideals)戴德金整環的全分式理想群的子群.設P(R)表示戴德金整環的一切非零主分式理想的集合。
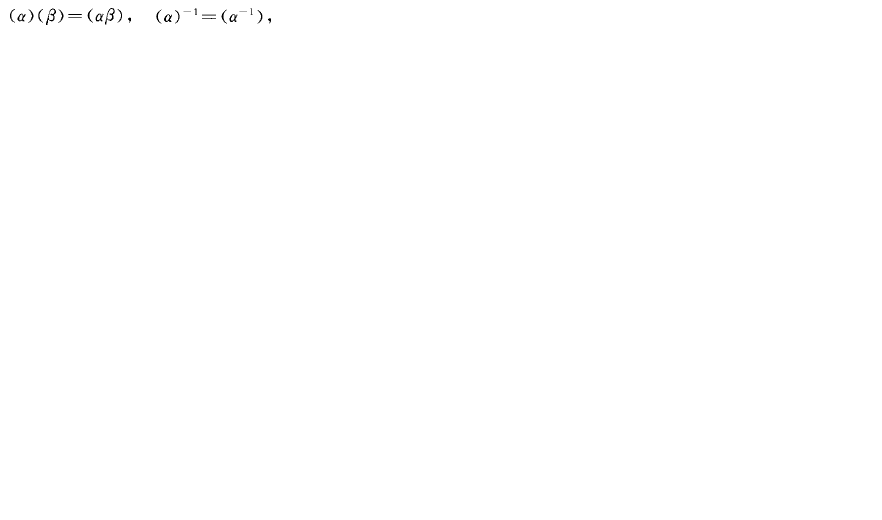
主分式理想群(group of principal fractionalideals)戴德金整環的全分式理想群的子群.設P(R)表示戴德金整環的一切非零主分式理想的集合。...
理想類群(ideal class group)是數域的分式理想群按主理想子群分類所形成的群。數域K的兩個分式理想A和B稱為等價的,指存在α∈K使A=αB。K的分式理想等價類...
分式理想(fractional ideal)是比理想更廣的一種理想。它由整環的商域中元構成。設K是整環R的商域。若X是R模K的子模,並且存在K中非零元β使得βXR,則稱X為...
當R是戴德金環時,R中每個非零分式理想都是可逆理想,因此,G(R)構成一個群,稱G(R)為R的全分式理想群。於是,整環R是戴德金環的充分必要條件是G(R)為乘法...
可以證明,K 中全體非零的分式理想在乘法下成一群,而且每個分式理想A 都可以唯一地表成素理想方冪的乘積(公式4)這個群稱為K的理想群,記為IK。...
戴德金整環OK中每個理想如何分解成素理想之積,是代數數論的一個重要研究課題。②D中全體主分式理想(α)(0≠α∈F,F為D的商域)形成I(D)的一個子群P(D)...
設 k是一數域,I是k的一切非零的分式理想構成的乘法群,I也記作l(k)。對於k上的任一阿貝爾擴張K,存在I的一個狹義子群h與K對應,使得k的每個素理想P在K中...
整環皮卡群(Picard group of an integral do-main )刻畫整環性質的一類阿貝爾群.它在代數K理論中有重要套用.它同構於由該環可逆分式理想的同構類按運算<1)(J...
。戴德金整環的性質保證此結構是一個群,換言之,任何非零分式理想皆可逆。若一理想 可由某元素 生成,則稱之主理想;可采類似辦法定義主分式理想。此外...
群定理(group theorem)類似於戴德金環的容許理想理論。...... 群定理(group theorem)類似於戴德金環的容許理想理論.設K是整閉整環R的商域.將R的一切非零分式...