不變對稱雙線性函式,數學術語。
基本介紹
- 中文名:不變對稱雙線性函式
- 所屬學科:數學
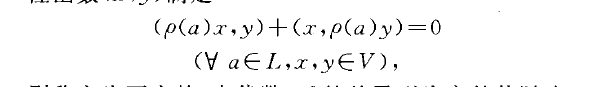
不變對稱雙線性函式,數學術語。
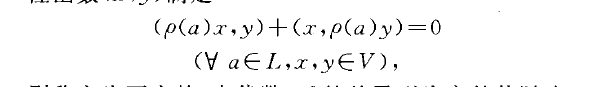
不變對稱雙線性函式,數學術語。不變對稱雙線性函式(invariant symmetric bi-linear function)定義在李代數上的一種雙線性函式.設(V,川為李)代數丫之表示,若V上對稱雙線性函式(二,y)...
對稱雙線性函式(symmetric bilinear function )一類特殊的映射函式。定義 如果線性空間V中,雙線性函式f(α,β)滿足:V中任意向量α,β都有:f(α,β)=f(β,α),則該雙線性函式f(α,β)稱為對稱雙線性函式。性質 對...
2.V上的雙線性函式φ關於不同基的矩陣A,B相互契約:A=XBX,其中X是原基底到新基底的過渡矩陣。3.φ關於基的矩陣(a)的秩亦稱為φ的秩。4.當(a)非退化時,φ亦稱為非退化的或滿秩的。5.當(a)為對稱(反對稱)矩陣時,φ...
酉空間的概念 8.2 複方陣的酉相似 8.3 正定Hermite方陣與矩陣的奇異值分解 8.4 一些例子 第9章 雙線性函式 9.1 雙線性函式的概念 9.2 對稱雙線性函式與二次型 9.3 斜對稱雙線性函式 9.4 共軛雙線性函式與 Hermite 型 ...
跡形式亦稱不變對稱雙線性形式,是線性空間中的雙線性函式的推廣。設A是域F上一個非結合代數,是A上(作為線性空間)的一個雙線性形式,若還有 ,則稱這個雙線性形式是跡形式。在非結合代數A上給定一個跡形式後,對A的每個理想B,得...
9.4.3 (反)對稱雙線性函式 第七章 Jordan標準形 7.1 最小多項式 7.1.1 最小多項式的概念和性質 7.1.2 最小多項式的計算 7.1.3 廣義特徵子空間分解 7.2 Jordan-Chevalley分解 7...
二、線性變換矩陣可對角化的條件 三、線性變換的不變子空間 四、商空間中的誘導變換 練習題3.4 第四章 雙線性函式與二次型 §1 雙線性函式 一、雙線性函式的定義 二、對稱雙線性函式 練習題4.1 §2 二次型 練習題4.2 §3...
§7.12線性函式,對偶空間 7.12.1內容精華 7.12.2典型例題 習題7.12 補充題七 第八章雙線性函式和二次型 §8.1雙線性函式 8.1.1內容精華 8.1.2典型例題 習題8.1 §8.2對稱雙線性函式與斜對稱 雙線性函式 8.2.1內容...
§6.13 線性函式,對偶空間 392 補充題六 398 第七章 雙線性函式,二次型 401 §7.1 雙線性函式的表達式和性質 402 §7.2 對稱和斜對稱雙線性函式 409 §7.3 雙線性函式空間,Witt消去定理 419 閱讀材料5 雙線性函式的秩 ...
8.5正交變換 8.6對稱變換 8.7二次型的主軸問題 8.8歐氏空間理論的套用——最小二乘法 8.9:酉空間簡介 第9章雙線性函式 9.1線性函式及性質 9.2對偶空間 9.3雙線性函式 9.4對稱雙線性函式 參考文獻 ...
第10章 雙線性函式與辛空間 10.1 知識脈絡圖解 10.2 重點、難點解讀 10.3 典型例題解析 10.3.1 線性函式及其對偶空間 10.3.2 雙線性函式及其度量矩陣 10.3.3 對稱雙線性函式的判定及度量矩陣的化簡 10.3.4 反對稱雙線性...
209 7.4 內積空間的線性變換 215 7.5 正交補與極小化問題 220 第8章 二次型 224 8.1 對稱雙線性函式與二次型 224 8.2 矩陣的契約及二次型的標準形 227 8.3 半正定矩陣與半正定二次型 234 參考文獻 240 索引 ...
第13章 雙線性函式 13.1 線性函式 13.2 對偶空間 13.3 雙線性函式 13.4 對稱與反對稱雙線性函式 習題13 第14章 基本代數結構簡介 14.1 代數運算 14.2 群及其基本性質 14.2.1 群的定義與例 14.2.2 群的基本性質...
