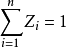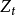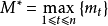不等機率抽樣是指在抽取樣本之前給總體的每一個單元賦予一定的被抽中機率。不等機率抽樣分為放回與不放回兩種情況。有放回的不等機率中，最常用的是按總體單元的規模大小來確定抽選的機率。不放回的不等機率抽樣，是指在抽樣的過程中被抽中的單元不能再被抽中，因此在抽取了第一個單元之後，餘下的N-1的單元中再以什麼樣的機率抽選就比較複雜。接著抽取第三和第四個單元時就面臨更複雜的問題，因此抽樣的實施比較困難。這種抽樣要求做到第j個單元入樣機率為πj，在樣本容量為n時所有N個單元的入樣機率之和就應等於n。
基本介紹
- 中文名：不等機率抽樣
- 外文名：sampling with unequal probability
- 所屬學科：數學
- 所屬問題：統計學（抽樣技術）
- 分類：有放回和無放回的的不等機率抽樣
不等機率抽樣的機率與特點,不等機率抽樣的種類,放回不等機率抽樣,不放回不等機率抽樣,區域抽樣,多項抽樣與PPS抽樣,πPS抽樣,不等機率抽樣的實施方法,代碼法,拉希里法,
不等機率抽樣的機率與特點
簡單隨機抽樣中，總體中的每個單元具有同樣的入樣機率，它們是等機率抽樣，在分層隨機抽樣中，層內單元是按簡單隨機抽樣抽取的，因此，它們也是等機率抽樣。等機率抽樣的特點是總體中每個單元地位相同，在抽樣時對每個單元採取“不偏不倚”的態度。
與等機率抽樣對應的另一類方法是不等機率抽樣，也就是在抽樣前賦予總體每個單元一個入樣機率，當然這個人樣機率是不相同的，否則抽樣就成為等機率的抽樣。
當總體單元之間差異不大時，簡單隨機抽樣也是簡便的、有效的。例如，對家庭消費支出的調查中，以家庭為抽樣單元，由於家庭之間的差異不是很大，因此用簡單隨機抽樣也是有效的。
當總體單元之間差異非常大時，簡單隨機抽樣效果並不好。例如，對船舶運輸量進行調查時，以船舶為抽樣單元，則有的是從事遠洋運輸的萬噸巨輪，更多的是從事內河河網運輸的上百噸乃至幾十噸小船，這對，簡單隨機抽樣的效果肯定不好。
出現總體單元差異特別大的情況時，通常是犧牲“簡單”來提高抽樣效率的。一種做法是將總體單元按規模(大小)分層，對較大單元的層抽樣比定得高些，抽樣比甚至是i00%，而較小單元的層抽樣比定得低一些。另一種做法就是賦予每個單元與其規模(或輔助變數)成比例的入樣機率，這樣以來，大單元入樣機率大，小單元入樣機率小。
實際工作中，如果遇到下面幾種情況，則可以考慮使用不等機率抽樣。
1．樣本單元在總體中所占的地位不一致。
例如上面所討論的船舶等調查問題。
2．調查的總體單元與抽樣總體單元不一致。
例如某大型單位準備對職工家庭進行調查，一種自然的辦法就是以人事部門的職工花名冊作為抽樣框進行抽樣，該單位有少數家庭兩名職工在該單位工作，如果對職工進行簡單隨機抽樣，則雙職工家庭被抽中的機率大，而調查者希望對家庭進行等機率抽樣。除了對抽樣框進行整理，將雙職工家庭中的一名成員從抽樣框拿掉以外，可以對職工採用不等機率抽樣，一種做法是對每名職工記錄其家庭成員在該單位工作的人數，然後對每名職工按與人數成反比的機率進行抽樣。
3．改善估計量。
不等概抽樣可用於對估計量進行改善，例如簡單隨機抽樣比率估計量是漸進無偏的，要使它成為無偏估計，只要每個大小為n的樣本被抽中的機率與其輔助變數的和
成比例(如水野法)，則這時的比率估計就是無偏估計量，而這個樣本並不是簡單隨機樣本，而是一個不等機率抽樣獲得的樣本。
不等機率抽樣的種類
放回不等機率抽樣
每次在總體中對每個單元按入樣機率進行抽樣，抽取出來的樣本單元放回總體，然後進行下一次抽樣。這樣的話，每次抽樣過程都是對同一個總體獨立進行的。放回不等機率抽樣實施及推算過程相對來說比不放回的簡單。
不放回不等機率抽樣
每次在總體中對每個單元按入樣機率進行抽樣，抽取出來的樣本單元不再放回總體，對總體中剩下的單元進行下一次抽樣。不放回不等機率抽樣的效率比放回時的效率高，但是不放回不等機率抽樣的實施及推算過程比放回時複雜得多。
對於不放回不等機率抽樣，樣本的抽取可以有以下幾種方法：
1．逐個抽取法
每次從總體未被抽中的單元中以一定的機率抽取一個樣本單元，通常這個機率與已被抽中的樣本單元有關。
2．重抽法
以一定的機率逐個進行放回抽樣，如果抽到重複單元，則放棄所有抽到的樣本單元，重新抽取，直至抽到規定的樣本量且所有樣本單元不重複。
3．全樣本抽取法
對總體每個單元分別按一定機率決定其是否入樣。這種方法的樣本量是隨機的，事先不能確定，而且它可能出現總體中全體單元都人樣或全都未入樣。
4．系統抽樣法
將總體單元按某種順序排列，將規定的入樣機率匯總，根據樣本量確定抽樣間距k，在1～k產生一個隨機數，並確定相應的初始單元，以後在總體中每隔忌個單元抽出一個作為樣本單元。
區域抽樣
區域抽樣也稱為面積抽樣。這種方法主要用於以下的情形：區域或面積本身就是抽樣單元，或者抽樣單元的名單抽樣框無法獲得，但每個抽樣單元只隸屬於某個區域。例如，某縣進行小麥產量調查時，將全縣農田土地按易於劃分的規則劃分成地塊(如利用溝渠、水渠、道路等地理特徵自然隔離)。然後對地塊進行抽樣，對被抽中地塊的小麥產量進行實割實測，從而推算全縣的產量。由於地塊的面積通常不相等，因此對地塊的抽樣可以是簡單隨機抽樣，也可以按地塊的面積進行不等機率抽樣。
為此，需要對抽樣框類型進行討論。抽樣框可以分為名單抽樣框和區域抽樣框。
名單抽樣框由抽樣單元組成。例如，某高校全體在校學生的花名冊就是一個名單抽樣框。又如，在工商管理部門登記的企業名冊也是一個名單抽樣框。
區域抽樣框由定義明確的區域組成，而一個區域是由個體組成的。例如，我們對居民家庭進行某項調查時，可以利用地圖編制各行政區的名單，或到街道辦事處獲得居委會的名單，這時的行政區及居委會都是由個體(居民戶)組成的區域，又如將農田土地劃分成地塊。
一般來說，抽樣調查的總體比較大，要編制全體抽樣單元的名單往往很困難，而且也沒有必要。這時比較容易的做法是通過對區域的劃分，建立區域抽樣框，然後對被抽中的區域進行調查，或者再編制下一階段的抽樣框。如果有必要，這個抽樣框也可以是區域抽樣框。
區域抽樣框有以下主要優點：
1．容易定義和識別
區域抽樣框很容易通過地圖或行政區加以定義，而且能很清楚地識別。
2．比較穩定
區域相對來說比較穩定。例如，我們調查一個居民樓中的所有居民戶，比利用居民戶名單抽樣框要容易得多，因為前者是穩定的，而後者可能在調查的時候已經搬遷。
3．容易操作，回答率較高
現場工作人員能很容易並清楚地識別和確定區域的界限，從而比較容易地找到樣本單元，使回答率提高。
多項抽樣與PPS抽樣
設
是一組機率，
，按這組機率對總體中的N個單元進行放回抽樣，每次抽中第i個單元的機率為
，獨立地進行這樣的抽樣n次，則這種不等概抽樣為多項抽樣。
特別地，如果每個單元有說明其大小或規模的度量M1，則
由於抽樣是放回的，因此，某個單元可能在樣本中出現多次，出現這種情況時，對這個單元的調查只進行一次，但計算時按抽中幾次計算幾次的原則進行。
πPS抽樣
對於放回抽樣，對總體參數的估計及其方差估計比較簡單，但樣本單元中可能有單元被抽中多次。直觀上看，沒有必要對同一個單元調查多次，因此放回抽樣得到的樣本代表性比不放回抽樣差。類似於簡單隨機抽樣的討論，在同樣樣本量的條件下，放回抽樣的估計量精度較低，尤其當抽樣，比不能忽略時，稱不放回的與單元大小成比例的機率抽樣為πPS抽樣。
不等機率抽樣的實施方法
代碼法
在PPS抽樣中，賦予每個單元與M1相等的代碼數，將代碼數累加得到M0，每次抽樣都產生一個[1，M0]之間的隨機數，設為m，則代碼m所對應的單元被抽中。
如果Mi不是整數，則乘以某個倍數。對於一般的多項抽樣，通常可以找到某個M0，使M0Z1為整數，每個單元賦予與M0Z1相等的代碼數，然後進行抽樣。
拉希里法
令
，即所有Mt中最大值，每次抽樣都分別產生一個[1，N]之間的隨機數i及[1，M*]之間的隨機數m，如果Mt≥m則第i個單元被抽中；否則，重抽一組(i，m)。
