基本介紹
- 中文名:不確定型有窮自動機
- 外文名:non-deterministic finite automata
- 適用範圍:數理科學
- 類型:有窮級數模型
簡介
引入
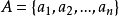
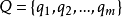
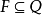

 圖1.有窮自動機
圖1.有窮自動機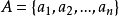
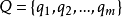
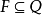

 圖1.有窮自動機
圖1.有窮自動機有窮自動機的每一步操作都是確定的,因此可稱為確定型有窮自動機。如果允許在每一步上讀頭的內部狀態可在幾個狀態中任取,即δ 之值為內部狀態之集合(而不是...
有窮自動機的每一步操作都是確定的,因此可稱為確定型有窮自動機。確定有窮自動機就是說當一個狀態面對一個輸入符號的時候,它所轉換到的是一個唯一確定的狀態...
其內容特點是抽象和形式化,既有嚴格的理論證明,又具有很強的構造性,從而培養...第3章有窮狀態自動機863.1語言的識別863.2有窮狀態自動機893.3不確定的有...
第3章 有窮狀態自動機3.1 語言的識別3.2 有窮狀態自動機3.3 不確定的有窮...9.2.5 其他圖靈機9.3 通用圖靈機9.4 幾個相關的概念9.4.1 可計算性...
第3章有窮狀態自動機543.1語言的識別553.2有窮狀態自動機553.3不確定的有...10.2線性有界自動機及其與上下文有關文法的等價性22310.3小結22510.4典型習題...
3.2有窮狀態自動機463.3不確定的有窮狀態自動機513.3.1作為對DFA的修改51...5.2正則語言的封閉性855.3Myhill Nerode定理與DFA的極小化89...
其內容特點是抽象和形式化,既有嚴格的理論證明,又具有很強的構造性。敘述中...3.2有窮狀態自動機723.3不確定的有窮狀態自動機833.3.1作為對DFA的修改83...
11.6 自動證明機器原型之五:不確定型有窮自動機15011.7 自動機接受的語言15311.8 自動機與數學證明的關係15511.9 定理證明器和推理機基本原理和證明實例156...
目標代碼生成、代碼最佳化技術、並行性檢測以及過程間分析技術,並在相關章節中給出...3.6 有窮自動機3.6.1 不確定的有窮自動機3.6.2 轉換表3.6.3 nfa接受輸入...
3.6.4 正則表達式與有窮自動機的等價性473.6.5 確定的有窮自動機的化簡49 [3] 3.6.6 根據DFA構造詞法分析程式513.7 詞法分析程式的自動生成器LEX52...
2.1.7 確定的有窮自動機的化簡2.1.8 正規式和有窮自動機的等價性2.2 典型例題解2.3 習題及解答第3章 文法和語言3.1 重點知識回顧...
3.5 有窮自動機3.5.1 不確定的有窮自動機3.5.2 轉換表3.5.3 自動機中輸入...4.1.2 代表性的文法4.1.3 語法錯誤的處理4.1.4 錯誤恢復策略4.2 上下文無關...
式的等性 4.3 有窮自動機 4.3.1 確定的有窮自動機(DFA) 4.3.2 不確定的有窮自動機(NFA) 4.3.3 NFA轉換為等價的DFA 4.3.4 確定有窮自動機的化簡 4.4 ...
