不相關變數是指兩個變數的相關係數為0的變數,是相互間沒有線性關係的變數。兩個變數是不是相關變數需要用相關係數r來判定,相關係數是用以反映變數之間相關關係密切程度的統計指標。
基本介紹
- 中文名:不相關變數
- 外文名:uncorrelatedvariable
- 學科:數學
- 判定方式:相關係數
- 基本釋義:相關係數為0的兩個變數
- 套用:判斷變數間是否存線上性關係
基本概念
判定方式
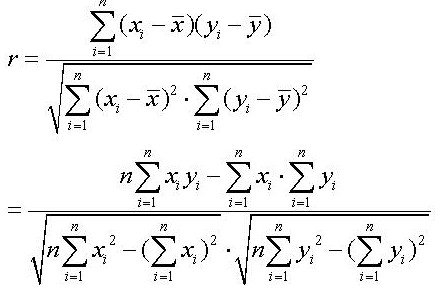

不相關變數是指兩個變數的相關係數為0的變數,是相互間沒有線性關係的變數。兩個變數是不是相關變數需要用相關係數r來判定,相關係數是用以反映變數之間相關關係密切程度的統計指標。
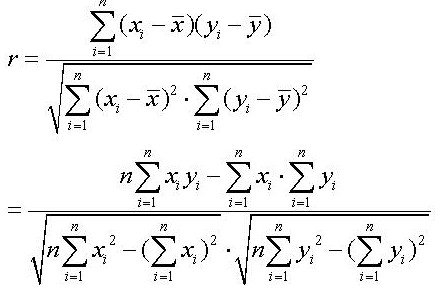
不相關變數是指兩個變數的相關係數為0的變數,是相互間沒有線性關係的變數。兩個變數是不是相關變數需要用相關係數r來判定,相關係數是用以反映變數之間相關關係密切程度的統計指標。基本概念不相關變數是指兩個變數的相關係數為0的變...
不相關隨機變數(uncorrelated random variables)是一類隨機變數,是指相互間沒有線性關係的隨機變數。如果隨機變數ξ,η的相關係數r=0,則稱ξ,η不相關。顯然,如果ξ,η相互獨立,則必定不相關。且下述事實等價:1.ξ,η不相關,...
零相關亦稱“不相關”。相關的一種。兩個變數的相關係數r=0時的相關。零相關表示兩個變數非線性相關,這時兩個變數可能相互獨立,也可能曲線相關。對於正態變數,兩個變數零相關與兩個變數相互獨立等價。對於一般情形,兩個變數相互獨立...
相關性,是指兩個變數的關聯程度。一般地,從散點圖上可以觀察到兩個變數有以下三種關係之一:兩變數正相關、負相關、不相關。如果一個變數高的值對應於另一個變數高的值,相似地,低的值對應低的值,那么這兩個變數正相關。在土壤...
曲線相關(curve correlation)亦稱“非線性相關”。在兩個變數單相關場合,其散點圖散布於某條曲線附近,進行回歸分析時宜用非線性回歸模型代表其間的相關關係。測度曲線相關密切程度的指標,叫相關指數。相關指數的平方,仍然等於回歸總變差...
外生變數(exogenous variable)亦稱“輸入變數”。完全由經濟系統外部確定並輸入系統的變數,它只對系統產生影響而不受系統的影響。在經濟計量模型中,外生變數是與模型的隨機擾動項不相關的變數。通常,描述影響經濟系統運行的,技術、政治...
簡單相關是兩類變數之間線性或非線性的不確定的關聯關係,又稱二元相關、單相關。在簡單相關情形下,兩個變數之間相關關係,可能是正相關的或負相關的,或者是無相關的。無相關,亦稱零相關或完全不相關,其相反情形是完全相關。基本介紹...
在初等數學中,變數是表示數字的字母字元,具有任意性和未知性。把變數當作是顯式數字一樣,對其進行代數計算,可以在單個計算中解決很多問題。變數的概念也是微積分的基礎。通常,函式y = f(x)涉及兩個變數y和x,分別表示函式的值和...
非線性相關是指輸出和輸入既不是正比例也不是反比例的情形,例如如宇宙形成初的混沌狀態。簡單介紹 自變數與變數之間不成線性關係,而是成曲線或拋物線關係或不成為定量,則這種關係就叫做非線性關係。“線性”與“非線性”,常用於區別...
扣除係數 a 和 b 以 X' 和 Y' 都同 Z 不相關為準。設已經對變數 X、Y、Z 的方差歸一化,即 var(X) = var(Y) = var(Z) = 1。於是有 同理,扣除係數 b = r。於是等效數據點 X' 和 Y' 之間的相關係數為 將上...
分類變數(categorical variable)是說明事物類別的一個名稱,其取值是分類數據。如“性別”就是一個分類變數,其變數值為“男”或“女”;“行業”也是一個分類變數,其變數值可以為“零售業”、“旅遊業”、“汽車製造 業”等。簡介...
協方差為0的兩個隨機變數稱為是不相關的。性質 若兩個隨機變數X和Y相互獨立,則E[(X-E(X))(Y-E(Y))]=0,因而若上述數學期望不為零,則X和Y必不是相互獨立的,亦即它們之間存在著一定的關係。協方差與方差之間有如下關係:...
自由度(degree of freedom, df)指的是計算某一統計量時,取值不受限制的變數個數。通常df=n-k。其中n為樣本數量,k為被限制的條件數或變數個數,或計算某一統計量時用到其它獨立統計量的個數。自由度通常用於抽樣分布中。定義 統...
無偏性的含義是:由於未知參數的估計量是一個隨機變數,對於不同的樣本它有不同的估計量.這些估計量對於參數的真實取值,一般都會有偏差,要求不出現偏差幾乎是不可能的。但是,總希望在多次試驗中所得到的估計量的平均值與參數的真實值...
1.實驗條件,即不同的處理造成的差異,稱為組間差異。用變數在各組的均值與總均值之偏差平方和的總和表示,記作SSb,組間自由度dfb。2.隨機誤差,如測量誤差造成的差異或個體間的差異,稱為組內差異,用變數在各組的均值與該組內...
,即相關係數的平方。這一項也可以用在回歸分析中,那裡不適用相關係數。在這種情況下,乃是在總的項平方之和中歸屬於另一變數來源即自變數的部分的比率。疏遠係數(coefficient of alienation):非確定係數(非判定係數)給定為 它是總...
回歸分析只涉及到兩個變數的,稱一元回歸分析。一元回歸的主要任務是從兩個相關變數中的一個變數去估計另一個變數,被估計的變數,稱因變數,可設為Y;估計出的變數,稱自變數,設為X。回歸分析就是要找出一個數學模型Y=f(X),使得...
互不相關均是與 同分布的隨機變數。為了用矩陣表示上式,令:於是有 ,使用最小二乘法得到 的解 。其中,稱為 的偽逆。回歸係數 一般地,要求這個值大於5%。對大部分的行為研究者來講,最重要的是回歸係數。年齡增加1個單位,...
示例 SIM手機用戶滿意度與相關變數線性回歸分析 以SIM手機的用戶滿意度與相關變數的線性回歸分析為例,來進一步說明線性回歸的套用。從實踐意義講上,手機的用戶滿意度應該與產品的質量、價格和形象有關,因此以“用戶滿意度”為因變數,“...
