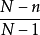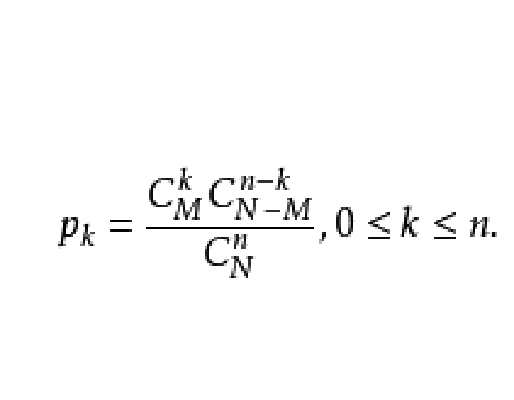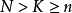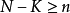基本介紹
- 中文名:不放回抽樣
- 外文名:sampling without replacement
- 別名:不重複抽樣
- 所屬學科:數學
- 相關概念:超幾何分布
定義,超幾何分布,例題引入,超幾何實驗的性質,超幾何分布的定義,
定義
不放回抽樣(sampling without replacement)即每次從總體中抽取一個單位,經調查記錄後不再將其放回總體中,因此,每抽一個單位,總體單位數就減少一個,每個單位被抽中的機率不同,如第一個樣本單位被抽中的機率為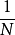 ,第二個單位被抽中的機率則為
,第二個單位被抽中的機率則為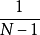 。
。
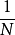
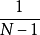
超幾何分布
例題引入
(不放回抽樣) 設一批產品共有N個,其中有M個次品。每次從這批產品中隨機地抽出一件來檢查,檢查後不放回,共取n次(相當於一次同時取n件產品),試求在n次檢查中有k次是次品的機率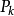 。從N件產品中抽取n件共有
。從N件產品中抽取n件共有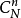 種不同的取法,現要求在抽取的一組n件產品中,有k件次品和n-k件合格品。因為這k件次品有
種不同的取法,現要求在抽取的一組n件產品中,有k件次品和n-k件合格品。因為這k件次品有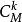 種不同的取法,n-k件合格品有
種不同的取法,n-k件合格品有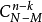 種不同的取法,故得
種不同的取法,故得
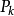
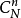
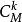
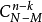
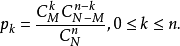
上式確定的分布律稱做超幾何分布,這是因為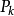 可看成是所謂超幾何級數的通項的係數。
可看成是所謂超幾何級數的通項的係數。
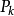
超幾何實驗的性質
超幾何分布是離散型隨機變數機率分布的一種,它是建立在超幾何實驗基礎之上的,若並非獨立的不重複試驗中,總體N中有“成功”類者為K個,失敗類者為N-K個,從總體中抽收n個作為樣本時,稱為超幾何實驗(如圖1所示)。
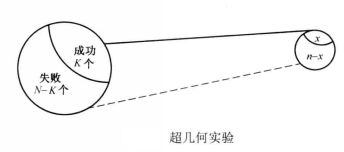 圖1
圖1超幾何實驗具有下列性質。
(1)從一個含有N個個體的總體中,以不重複方式隨機抽取n個作為樣本,各次試驗(抽樣)並非獨立的。
(2)總體N中成功類者為K個,失敗類者為N一K個。
(3)樣本中抽自成功類者為x個,抽自失敗類者為n-x個。
(4)由於不重複試驗(抽樣),每次試驗成功的機率受其前次試驗結果的影響,故成功的機率不能維持不變。
超幾何分布的定義
超幾何分布的定義為:若離散型隨機變數的分布具有下列機率函式,即
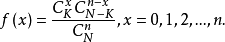
則稱為超幾何分布。
①期望值
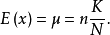
②方差
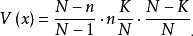
其中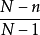 稱為有限總體校正因子,當採用不重複隨機抽樣時才須考慮,因而又稱不重複抽樣校正因子。
稱為有限總體校正因子,當採用不重複隨機抽樣時才須考慮,因而又稱不重複抽樣校正因子。