基本介紹
- 中文名：三角形的內接矩形
- 外文名：Inscribed rectangle of triangle
- 常考內容：求三角形內接矩形的最大面積
- 常用結論：最大面積為三角形面積的一半
三角形內接矩形的定義,三角形內接矩形的種類,三角形內接矩形的最大面積問題,相關結論,解決思路,結論證明,三角形內接矩形的其他結論,三角形內接正方形的相關結論,三角形內接矩形及其相關結論的套用,
三角形內接矩形的定義
三角形的內接矩形：若矩形的四個頂點都在三角形的邊上，則該矩形為三角形的內接矩形（即三角形的內接長方形）.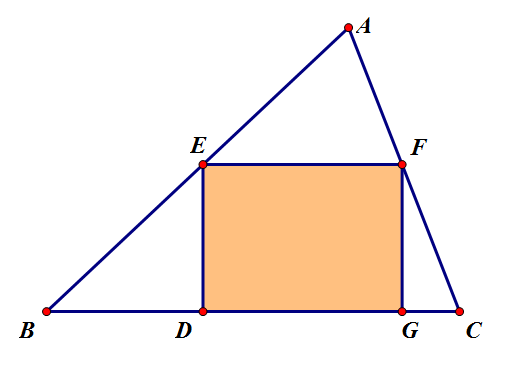
三角形內接矩形
三角形內接矩形的種類
直角三角形的內接矩形有兩種，銳角三角形的內接矩形有三種，而鈍角三角形只有一種.
三角形內接矩形的最大面積問題
三角形內接矩形的最大面積問題可被認為是三角形內接平行四邊形面積與原三角形面積關係結論的推論.三角形內接平行四邊形面積不大於原三角形面積的一半.
相關結論
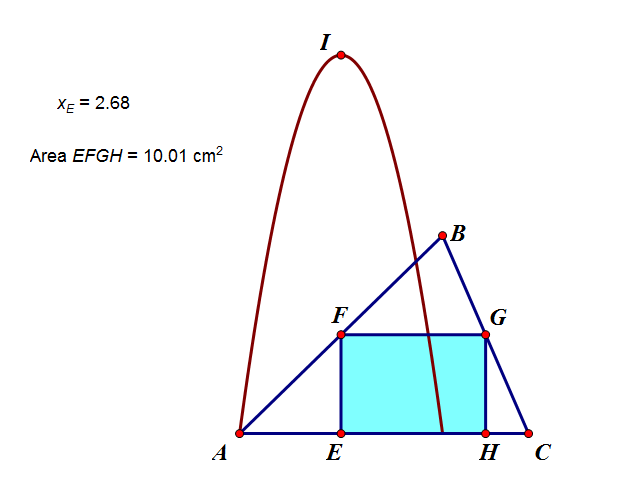
三角形內接矩形
三角形內接矩形的最大面積問題結論：當三角形的內接矩形的一邊長等於它所對的該三角形的邊長的一半時（也可認為當三角形內接矩形的一邊是三角形的一條中位線時），內接矩形的面積最大，最大面積等於該三角形面積的一半.
特別地，當直角三角形內接矩形的一邊長等於直角三角形斜邊或兩直角邊長的一半時（這取決於內接矩形的擺放方式），內接矩形的面積最大，最大面積等於該直角三角形面積的一半.
注意：三角形中最大面積的內接矩形不一定為正方形.
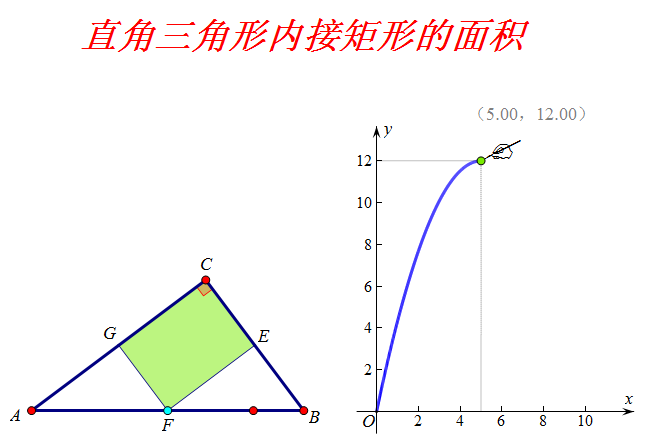
三角形內接矩形
解決思路
三角形內接矩形最大面積問題的求解是數形結合的典範，用到了相似三角形的性質、均值不等式、三角形面積公式等較為基礎的數學知識.這是一個典型的最最佳化問題，解決這類最大面積問題往往需要通過提公因式的方法構造出和一定的兩個式子的乘積，進而利用均值不等式（國小奧數里的“和一定，差小積大”原理）加以解決.
結論證明
如圖1所示，不失一般性，設四邊形DEFG為三角形ABC的內接矩形，過點A作AM垂直BC交BC於M，交DG於N.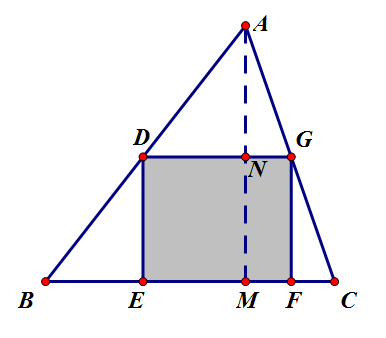
圖1 三角形內接矩形最大面積結論的證明
不妨設AM=a，BC=b，MN=DE=x，則易由線束定理得比例式
，由此可得
，即
，故有
.故內接矩形DEFG的面積為
，當
時，該式取得最大值，此時
，內接矩形的最大面積為
.故結論得證.
三角形內接矩形的其他結論
在限定內接矩形的高（平行於三角形一條邊上的高的邊）的情況下，只有當三角形一邊上的高等於內接矩形高的2倍，且內接矩形的一邊在這條邊上時，所得到的內接矩形的面積最大.
三角形內接正方形的相關結論
如圖2，設正方形DEFG為三角形ABC的內接正方形，過點A作AM垂直BC交BC於M，交DG於N（如圖2），則易由相似三角形推出
.
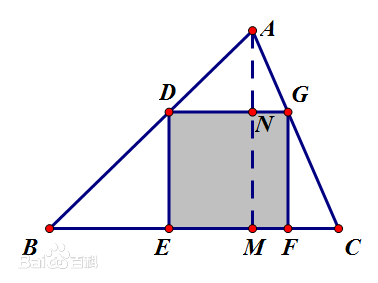
圖2
三角形內接矩形及其相關結論的套用
有關三角形內接矩形的問題在初等數學中有著廣泛的套用.
例1：已知△ABC，若AB=2，BC=12，AC=10，要把它加工成矩形零件，若矩形一邊分別在AB、AC、BC上，其餘兩頂點在另兩條邊上，問在哪一邊上截得最大面積的矩形？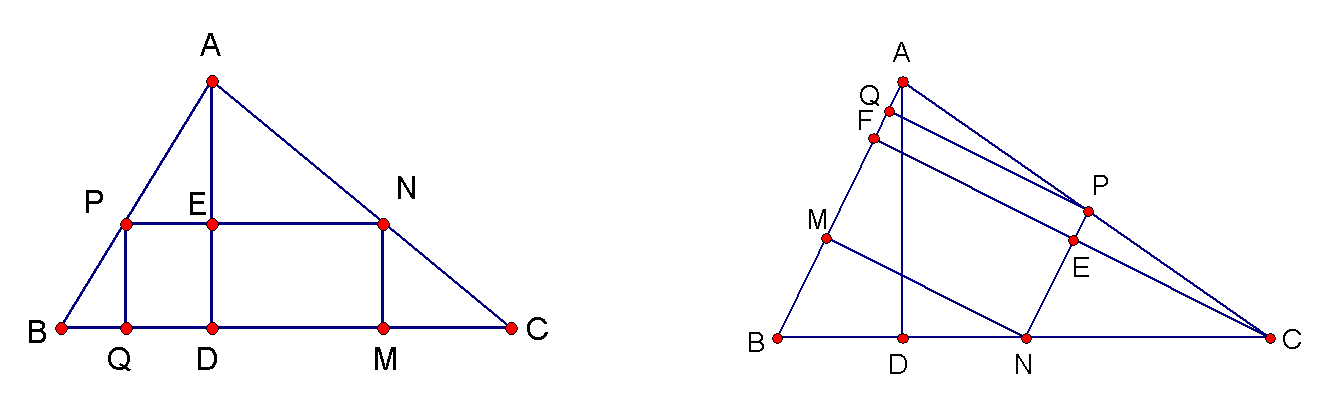
圖3
解題突破口：分類討論三種情況，利用上述結論即可.
例2：如圖3，有一塊三角形余料ABC，它的邊BC=120mm，高線AD=80mm，要把它加工成矩形零件，使矩形的一邊在BC上，其餘兩個頂點分別在AB、AC上，當矩形PQMN與△ABC的面積之比為3∶8時，求矩形PQMN的周長.
解題突破口：表示內接矩形的面積，然後根據題目條件進行解決.
例3：如圖4，在一個直角三角形的內部作一個矩形ABCD，其中AB和AD分別在兩直角邊上，AF=40m，AE=30m.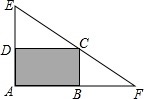
圖4
(1)如果設矩形的一邊AB=xm，那么AD邊的長度如何表示?
(2)設矩形的面積為y平方米，當x取何值時，y的值最大?最大值是多少?
解題突破口：直接運用上述結論即可.
例4：為探究三角形內接矩形的最大面積，小明做了若干次試驗.
【探索發現】
如圖5中①,是一張直角三角形紙片,∠B=60度，小明想從中剪出一個以∠B為內角且面積最大的矩形，經過多次操作發現，當沿著中位線DE、EF剪下時，所得的矩形的面積最大，隨後，他通過證明驗證了其正確性，並得出：矩形的最大面積與原三角形面積的比值為___.
【拓展套用】
如圖5中②,在△ABC中,BC=a,BC邊上的高AD=h,矩形PQMN的頂點P、N分別在邊AB、AC上,頂點Q、M在邊BC上,則矩形PQMN面積的最大值為___.(用含a,h的代數式表示)
【靈活套用】
如圖5中③,有一塊“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明從中剪出了一個面積最大的矩形(∠B為所剪出矩形的內角)，求該矩形的面積.
【實際套用】
如圖5中④,現有一塊四邊形的木板余料ABCD,經測量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=4:3，木匠徐師傅從這塊余料中裁出了頂點M、N在邊BC上且面積最大的矩形PQMN，求該矩形的面積.
解題突破口：通過構造輔助線將不規則圖形進行轉化即可.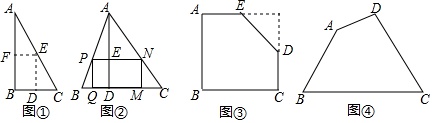
圖5
