一階差分就是離散函式中連續相鄰兩項之差。當自變數從x變到x+1時,函式y=y(x)的改變數∆yx=y(x+1)-y(x),(x=0,1,2,......)稱為函式 y(x)在點x的一階差分,記為∆yx=yx+1-yx,(x=0,1,2,......)。
基本介紹
- 中文名:一階差分
- 外文名:feasible region
- 所屬學科:離散數學
- 相關概念:差分、差分方程
基本概念
定義
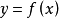







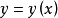




例題解析
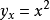


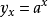






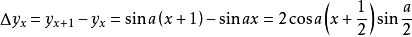
高階差分





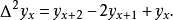




差分的性質及定理
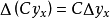
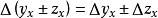






差分方程









一階差分就是離散函式中連續相鄰兩項之差。當自變數從x變到x+1時,函式y=y(x)的改變數∆yx=y(x+1)-y(x),(x=0,1,2,......)稱為函式 y(x)在點x的一階差分,記為∆yx=yx+1-yx,(x=0,1,2,......)。
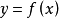







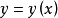




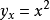


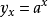






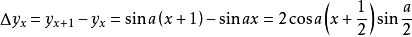





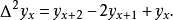




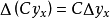
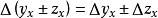














一階差分就是離散函式中連續相鄰兩項之差。當自變數從x變到x+1時,函式y=y(x)的改變數∆yx=y(x+1)-y(x),(x=0,1,2,...)稱為函式 y(x)...
當自變數從x變到x+1時,函式y=y(x)一階差分的差分Δ(Δy(x))=Δ(y(x+1) - y(x))=Δy(x+1) - Δy(x)=(y(x+2) - y(x+1)) - (y(...
在數學中,差分法(difference methods,簡稱DM),是一種微分方程數值方法,是通過有限差分來近似導數,從而尋求微分方程的近似解。“差分法”是在比較兩個分數大小時,...
中心差分及一階迎風格式優缺點的討論:1、在對流項中心差分的數值解不出現振盪的參數範圍內,在相同的格線節點數下,採用中心差分的計算結果要比採用迎風差分的結果...
差分,又名差分函式或差分運算,差分的結果反映了離散量之間的一種變化,是研究離散數學的一種工具,常用函式差近似導數。差分在數學、物理和信息學中套用很廣泛,...
當離散系統的特性可以用“一階差分方程”描述時,這種離散系統就被稱之為“一階離散系統”。...
中心差分法是指結構動力學中的中心差分法是基於用有限差分代替位移對時間的求導,對位移一階求導得到速度,對位移二階求導得加速度。...
有限差分方法(finite difference method)一種求偏微分(或常微分)方程和方程組定解問題的數值解的方法,簡稱差分方法。...
設有序列f(k), 則稱...f(k+2),f(k+1),...f(k-1),f(k-2)...等為f(k)的移位序列 一階前向差分定義為 △稱為差分運算元; 二階前向差分定義...
差商即均差,指導數的近似值。對等步長(h)的離散函式f(x),其n階差商就是它的n階差分與其步長的n次冪的比值。例如n=1時,若差分取向前的或向後的,所得一...
