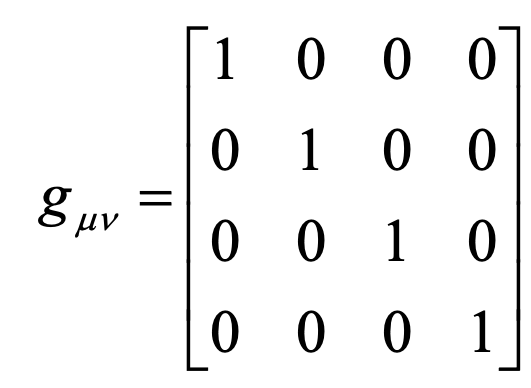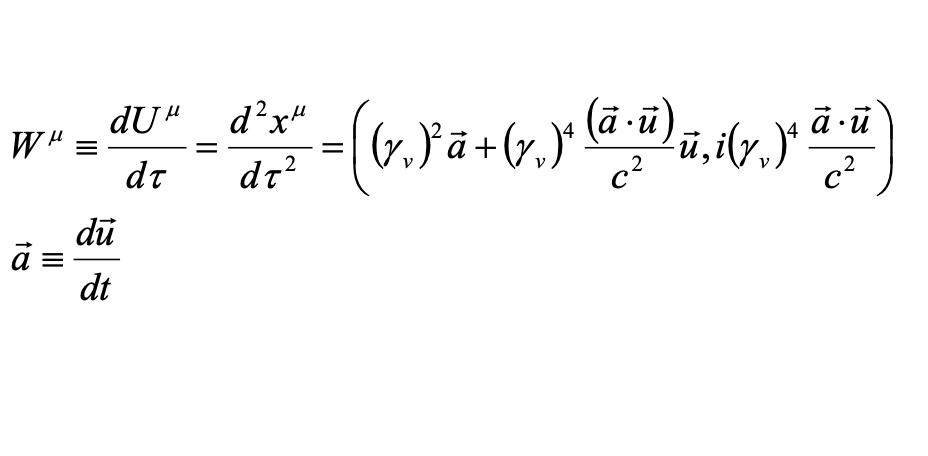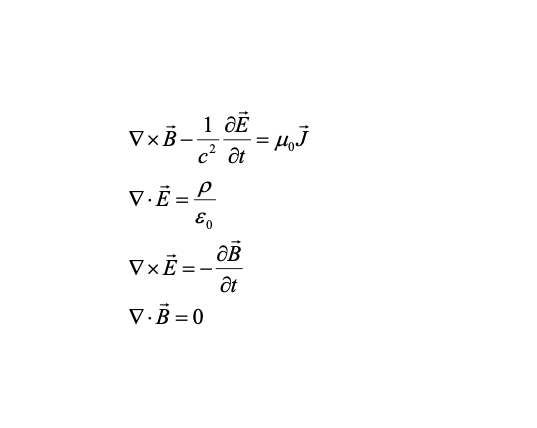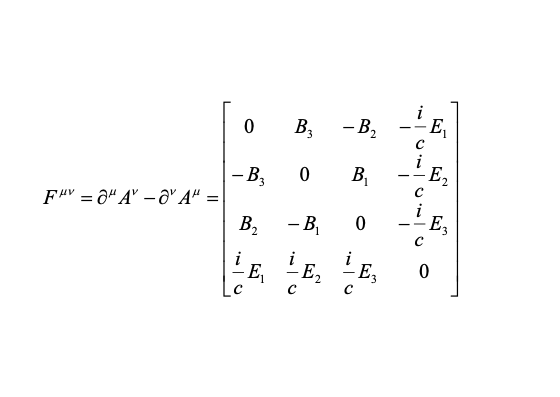阿爾伯特·愛因斯坦在分析了以太假說的矛盾後，於1905年在《論動體的電動力學》中提出了兩條基本原理：狹義相對性原理和光速不變原理，並據此建立了狹義相對論（Special Theory of Relativity）。
區別於牛頓的絕對時空觀，狹義相對論將時間和空間與觀測者視為一個不可分割的整體。相對桿和鐘分別靜止和勻速運動的觀測者，在測量同一根桿的長度以及比較同一個鐘的快慢時會得出不同的結論，這一現象被稱為“尺縮”和“鐘慢”效應，它們是狹義相對論的必然後果。
狹義相對論的核心不是相對性，而是保證物理規律的協變性。
狹義相對論的數學表述是洛倫茲變換（Lorentz transformation），幾何語言是時空圖（spacetime diagram）。
迄今為止，狹義相對論已經得到許多高精度實驗的支持。
基本介紹
- 中文名：狹義相對論
- 外文名：special relativity
- 別名：特殊相對論
- 提出者：阿爾伯特·愛因斯坦
- 提出時間：1905年
- 適用領域：物理學、粒子物理
- 套用學科：現代物理學
- 論文：《論動體的電動力學》
理論動機,理論內容,基本原理,推論,實驗檢驗,對狹義相對論兩個基本原理的檢驗,時間膨脹的檢驗,檢驗橫向都卜勒效應,洛倫茲不變性的檢驗,極限速度的檢驗,電子的相對論質量變化的檢驗,對理論物理學的影響,狹義相對論的困難,
理論動機
早在1632年，伽利略就通過實驗指出：相對於慣性系做勻速直線運動的任一慣性系，力學規律是相同的。這一觀點在當時被廣泛接受，被稱為伽利略相對性原理。20世紀以前，物理學家的時空觀是絕對時空觀，反映不同慣性系之間時空坐標變換關係的公式是伽利略變換。伽利略相對性原理的數學表述自然是：在伽利略變換下，力學定律的形式不變。
對物理學家來說，伽利略相對性原理是不容質疑的，並且它是一個“管定律的定律”。凡是不滿足伽利略相對性原理的力學定律都是需要修改的。
直到19世紀，電磁學迅速發展，電磁學規律可簡單地概括為麥克斯韋方程組。出乎意料地是：麥克斯韋方程組在伽利略變換下不是協變的。
對當時的部分物理學家而言，麥克斯韋方程組違反了伽利略相對性原理，最明顯的道路是：修改麥克斯韋方程組以得到一個滿足伽利略協變性的電磁學定律。
對另一部分物理學家來說，麥克斯韋方程組同樣是被很多實驗證實的電磁學理論，也具有不可動搖的地位。一種方法是：犧牲伽利略相對性原理的普遍性，承認伽利略相對性原理只適用於力學規律而不能被推廣到電磁學的物理範疇；堅持麥克斯韋方程組是正確的，只不過麥克斯韋方程組中的c是電磁波相對一個特殊慣性系（當時稱為“以太”）的傳播速度，麥克斯韋方程組也只在這一參考系下成立。因為“以太”是一個未經證實的猜測，這部分物理學家的首要任務是證實以太的存在，並證明電磁波相對以太參考系的傳播速度為c。但是，對此進行的霍克實驗、菲佐實驗和邁克耳孫-莫雷實驗（Michelson-Morley Experiment）對v/c的一階效應和二階效應的實驗結果之間卻相互矛盾，使物理學家難以自圓其說。
在那個時代，只有愛因斯坦另闢蹊徑。首先，邁克耳孫-莫雷實驗的零結果使他堅信：真空中的光速與觀測者的速度無關，恆為c（提出光速不變原理）。這意味著麥克斯韋方程組在任何慣性參考系中都成立，無需修改；結合伽利略相對性原理，他猜測：任何物理規律（不管是電磁學規律還是力學規律）在慣性系下都是相同的（提出狹義相對性原理）。現在，麥克斯韋方程組不具有伽利略變換的協變性，這說明伽利略變換沒有正確地反映慣性系之間的時空坐標變換關係。因此，需要修改的是絕對時空觀和對應的伽利略變換。
理論內容
基本原理
狹義相對性原理：任何真實的物理規律在所有慣性系中應形式不變。
光速不變原理：任意一個慣性系中的觀測者所測得的真空中的光速恆為c。
推論
時空觀
由兩條基本原理可嚴格地導出慣性系之間時空坐標變換的方程組，即洛倫茲變換。與伽利略變換不同：
（1）相對地面靜止的S慣性系觀測到的同時事件在相對地面勻速運動的S’系看來是不同時的，即同時的相對性。
（2）同一根尺子，相對尺勻速運動的觀測者比相對尺靜止的觀測者測量的桿長要短，即尺縮效應。
（3）同一個鐘，相對其勻速運動的觀測者發現這個鐘比相對其靜止的情況下走得要慢，即鐘慢效應。
（4）空間間隔和時間間隔是相對的（在慣性系變換下是改變的），但時空間隔（line element）在洛倫茲變換下是不變的（光速不變原理的直接要求）。
（5）S慣性系觀測到的先後發生的兩個事件在相對其勻速運動的S’系看來這兩個事件的先後順序可能是顛倒的。
（6）如果假定互為因果關係的兩個事件在任何慣性系下都不可顛倒因果順序，結合狹義相對論可知:任何信號的傳播速度都不可能超過真空中的光速c。（5）可總結為：具有類空（spacelike）間隔的兩個事件的時間順序可以相互顛倒；具有類時（timelike）或類光（lightlike）間隔的兩個事件的時間順序不可顛倒。
在牛頓的絕對時空觀中，時間與空間是絕對的，與觀測者的運動狀態無關，並且時間與空間是相互獨立的。現在，狹義相對論否定了這個觀點。時間與空間是相對的，在慣性系變換下，它們都可能改變；時間與空間是不可分割的整體，它們一起構成的時空間隔在慣性系變換下是不變的。
對新理論的指導
狹義相對論將伽利略相對性原理提升到了更廣泛的範疇，物理學規律（不僅僅是力學規律）都應具有慣性系變換下的協變性。因此，判斷一個物理學定律是否正確，第一道門檻就是具有協變性（covariance）。考慮到，物理學定律大多是描述一些物理量的等式或不等式關係。顯然，對物理量按照其在慣性系變換下的變換規律進行分類（洛倫茲標量、洛倫茲矢量和洛倫茲張量）將方便判斷物理學定律的協變性。同時，這也為構造新的物理學定律指明了方向——只有特定的標量（scalar）、矢量（vector）、張量（tensor）的組合所構成的物理量才可能參與到特定的方程中。
（1）相對論力學
牛頓力學不是相對論協變的，必須修改。
首先，引入事件的概念：事件用P(x,y,z,t)表示，即空間的一點和時間的一瞬。四維位置矢量表示為，時空度規表示為：
最後，觀測並記錄點粒子的行為需要觀者。一個觀者只能對發生在自己世界線上的事件做直接觀測，若要對全時空的任何事件進行觀測，就需要處處設定觀者。若這些觀者的世界線處處彼此不相交並且能充滿整個時空，就構成了一個參考系（reference frame）。在所有觀者中，其世界線為類時測地線的觀者稱為慣性觀者（inertial observer），一個慣性觀者可藉助自己的世界線建立一個慣性坐標系，慣性坐標系的t軸重合於自己的世界線，垂直於由彼此正交的x、y、z軸構成的三維空間。
對應的固有時為
該粒子的四維速度（4-velocity）定義為
該粒子的四維加速度（4-acceleration）定義為
粒子受到的四維力（4-force）定義為
以上，
,
,
都是三維空間的概念，定義保持與牛頓力學相同；
都是四維洛倫茲矢量，分別稱為：四維力，四維速度，四維加速度。現在，注意到牛頓第二定律為：
該定律不是相對論協變的，現在將,等三維概念替換為
，
等四維物理量，得到一種協變的形式：
注意到：
比較空間和時間部分，得到：
即粒子的相對論運動方程，m是在粒子的瞬時慣性系測得的粒子質量，稱為固有質量（proper mass）或靜止質量。因為m在相對論力學中有特殊的含義，所以下面將一律採用表示固有質量。
若點粒子在運動中相對瞬時慣性系的質量不變（粒子不發生衰變），注意到以上空間部分的表達式可寫為
m稱為運動質量或相對論質量，
稱為相對論動量，是一個三維矢量。利用四維速度可構造一個四維洛倫茲動量，是其空間部分：
現在注意到以上時間部分的表述式
該式在牛頓力學（相對論低速近似）就是功能關係。
據此，稱
為相對論能量，即
該定義式稱為相對論質能關係，它的物理含義是:
1.物質系統所具有的總能量與總質量成正比
2.物質系統能量的變化與質量的變化成正比
3.能量是一個相對量，其與相對論動量可構成一個四維動量，能量在慣性系變化下會改變
4.在粒子的瞬時局域慣性系，粒子靜止，觀測到的粒子能量最小，但不一定等於零；換言之，粒子具有靜止能量（固有能量）
。
現在定義一個物理量
將的定義式代入功能關係，有
該式在牛頓力學（相對論低速近似）就是動能定理。
據此，稱為相對論動能。
（2）電動力學
電動力學的基礎是麥克斯韋方程組和洛倫茲力公式。
麥克斯韋方程組是：
在洛倫茲變換下，可以驗證，該方程組天生是協變的，無需修改；但是，引入電磁場張量（一個洛倫茲張量） 替換掉電場和磁場後可以更方便地看出其協變性
檢查等式各項的洛倫茲指標，可知麥克斯韋方程組具有洛倫茲協變性。
帶電粒子單位體元內（粒子的體元由粒子的瞬時慣性系測量，一般稱為固有體元，粒子的電荷和固有體元都是洛倫茲標量）在外電磁場中受到的洛倫茲力密度為：
該式就是洛倫茲力公式的四維表示，顯然是協變的。
我們只是將洛倫茲力公式和麥克斯韋方程組寫成了張量方程式，並沒有修改兩者，這說明電動力學是天生洛倫茲協變的。這是很自然的事情，因為狹義相對論的兩大基本原理建立在電磁理論符合相對性原理的前提上。一個慣性系的觀測者僅測得電場而無磁場，相對其勻速運動的另一觀測者卻可能測得磁場的存在。狹義相對論解釋了這一現象，電場和磁場是同一個統一客體-電磁場的不同側面。
補充:
1. 關於麥克斯韋方程組的協變性
這需要兩個假設：
是洛倫茲四矢量以及
是洛倫茲張量。
2. 關於
和
可構成一個洛倫茲四矢量
這是一個假設。
3.關於是一個洛倫茲張量
定義三維矢勢
和標勢
假設和構成一個洛倫茲四矢量
，那么
可見是一個洛倫茲張量，這基於一個假設：和構成一個洛倫茲四矢量
。
實驗檢驗
對狹義相對論兩個基本原理的檢驗
相關的實驗有:對光速各向同性的檢驗、由實驗約束光子靜止質量上限、檢驗光速與光源速度是否有關等。
時間膨脹的檢驗
相關高精細的實驗有很多，如利用快速光學原子鐘或利用穆斯保爾效應的高精度譜解析度等檢驗時間膨脹；在可接受的誤差範圍內，實驗結果與狹義相對論都是一致的。
檢驗橫向都卜勒效應
假設光源發射光信號的固有頻率（在光源的靜止慣性系檢測的頻率）為
，一個相對光源以速度運動的觀測者接收到的光信號頻率為
，觀測者的速度方向和光源運動方向的夾角為
。在狹義相對論中，光源的都卜勒效應（Doppler effect）可表示為
注意到
即使光源橫向運動，觀測者也將收到紅移（red shift）的光信號，這是在牛頓力學中不可能發生的。驗證橫向都卜勒效應是對狹義相對論的有力檢驗之一。
洛倫茲不變性的檢驗
擾動標準模型的拉格朗日量，使其對洛倫茲不變性有一個微小的偏離後，將會產生新的宇宙射線物理學和中微子物理學現象。相關的高能實驗能對其作出檢驗。
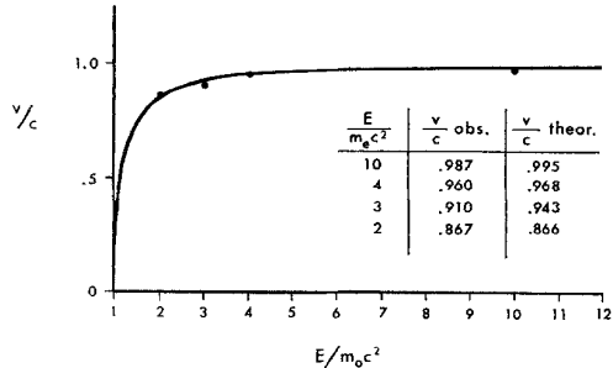
極限速度的檢驗
因果律和狹義相對論要求信號的極限速度為
圖中曲線是理論上的相對論速度-能量關係，實驗數據點的對象
介子。
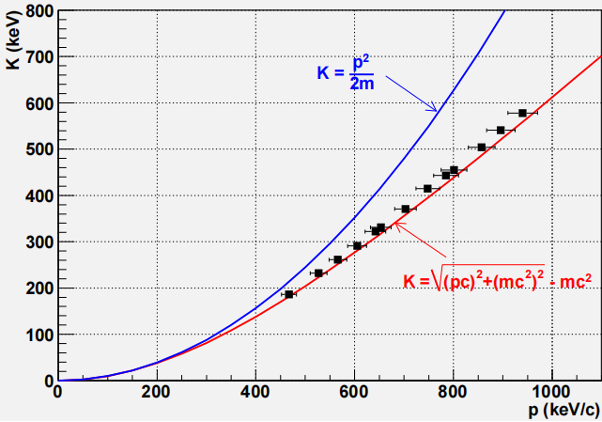
電子的相對論質量變化的檢驗
按照狹義相對論，電子質量m將隨速度增大而增大，可通過測量電子的動能與動量來間接檢驗。
紅色曲線是理論上的相對論動能-動量關係，藍色曲線是理論上的牛頓力學的動能-動量關係。從圖中可以看出，實驗數據點與紅色曲線較為吻合。
狹義相對論的相關實驗目前仍在進行，一部分原因是出於量子層面的，已經有許多量子引力和弦理論模型考慮了狹義相對論在接近普朗克尺度時被破壞的可能性。
對理論物理學的影響
在牛頓力學統治的時代，物理學家的主要研究對象是巨觀的力學系統，牛頓力學定律是在這一巨觀尺度上經驗總結和實驗推斷的結果。從電磁學現象的發現到狹義相對論的建立，研究對象的尺度發生改變，問題實際上涉及到高速運動的微觀粒子。狹義相對論就是在這裡發揮巨大威力的。比如，德布羅意利用相對論能量動量關係提出了物質波假設和德布羅意關係，托馬斯考慮了相對論運動學效應後才給出正確的自旋軌道耦合相互作用。
在狹義相對論中，信號傳播的極限速度是光速，相互作用只能是定域的，這一理念是愛因斯坦早期反對量子力學完備性的強烈理由。愛因斯坦的質疑推動了隱變數理論和貝爾不等式的檢驗，最終物理學家發現了量子力學的固有非定域特徵。
物理學家研究微觀世界，離不開量子場論，而量子場論是建立在量子力學和狹義相對論的基礎上的。
除了啟發和指導新理論，狹義相對論對物理學家思考問題的方式產生了深遠的影響。洛倫茲群反映連續的時空對稱性，它要求物理的拉氏量應具有時空轉動（boost）和空間旋轉不變性，這啟發物理學家去發現系統潛在的自由度和對稱性，如宇稱、同位旋、規範對稱性等。
狹義相對論的困難
在創立狹義相對論以後，愛因斯坦認識到該理論存在兩個嚴重的困難：
1. 狹義相對論在眾多的參考系中，承認了慣性參考系相比其他參考系具有優越性，物理學規律在所有慣性系中都是平權的；然而，慣性系本身卻無法被定義。
2. 愛因斯坦無法將萬有引力定律納入狹義相對論的框架，萬有引力定律無法被修改為洛倫茲協變的形式。
通過對這兩個困難的思考，愛因斯坦創立了廣義相對論。
