在定傳動比的齒輪傳動中,節點在齒輪運動平面的軌跡為一個圓,這個圓即為節圓。此時齒輪傳動可以認為兩個齒輪的節圓相切做純滾動。一對標準齒輪處在正確安裝位置時,即兩齒輪的分度圓相切時,此時的分度圓與節圓重合。
基本介紹
- 中文名:節圓
- 外文名:pitch circle
- 所屬學科:機械設計製造
- 本質:節點在齒輪運動平面的軌跡
- 作用:齒輪重要參數
- 辨別:節圓和分度圓
定義
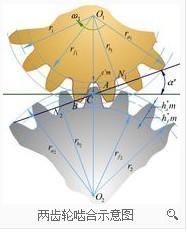

在定傳動比的齒輪傳動中,節點在齒輪運動平面的軌跡為一個圓,這個圓即為節圓。此時齒輪傳動可以認為兩個齒輪的節圓相切做純滾動。一對標準齒輪處在正確安裝位置時,即兩齒輪的分度圓相切時,此時的分度圓與節圓重合。

在定傳動比的齒輪傳動中,節點在齒輪運動平面的軌跡為一個圓,這個圓即為節圓。此時齒輪傳動可以認為兩個齒輪的節圓相切做純滾動。一對標準齒輪處在正確安裝位置時...
兩齒輪連心線上咬合接觸點各齒輪上留下軌跡稱為節圓,它的直徑就是節圓直徑。節圓直徑是齒輪參數中一個很重要的數字,齒輪上的很多數據都是與節圓直徑有關的,...
螺栓頭下一般製成凸台的樣式,稱為節圓。可以防止應力集中,增加支承面強度,保證不掉頭。 ...
與元宵節吃的湯圓即“上元圓”不同,冬至時吃的湯圓是沒有包裹內餡的,這種冬至湯圓也被叫做“冬節圓”。 在閩南地區,人們會把吃“上元圓”、“冬至圓”稱為...
節圓周長屬於學科專有名詞。...... 節圓周長詞條標籤: 文化 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:百科ROBOT...
中文名稱 蝸輪節圓 英文名稱 pitch circle of wormwheel 定義 蝸輪節圓柱面與中間平面的交線。 套用學科 機械工程(一級學科),傳動(二級學科),蝸桿傳動(三級...
中文名稱 滾子組的節圓直徑 英文名稱 pitch diameter of roller set 定義 軸承內一列滾子的中部,貫穿滾子軸心線的圓的直徑。 套用學科 機械工程(一級學科),...
在定傳動比的齒輪傳動中,節點在齒輪運動平面的軌跡為一個圓,這個圓即為節圓。此時齒輪傳動可以認為兩個齒輪的節圓相切做純滾動。一對標準齒輪處在正確安裝位置時...
中文名稱 節圓螺旋線 英文名稱 pitch helix 定義 斜齒輪的節圓柱面與齒面的交線。 套用學科 機械工程(一級學科),傳動(二級學科),齒輪傳動(三級學科) 以上...
蝸桿節圓屬於學科專有名詞。...... 蝸桿節圓詞條標籤: 文化活動 , 文化 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:百科ROB...
中文名稱 球組的節圓直徑 英文名稱 pitch diameter of ball set 定義 軸承內一列球的球心組成的圓的直徑。 套用學科 機械工程(一級學科),機械零件(二級學科...
齒廓接觸點的公法線與連心線的交點稱為節點,一對齒廓嚙合過程中節點在齒輪上的軌跡稱為節線,節線是圓形的稱為節圓。具有節圓的齒輪為圓形齒輪,否則為非圓形...
節徑應該是指節圓(分度圓)直徑。 ...... 節徑應該是指節圓(分度圓)直徑。V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:百...
基圓柱是由基圓擴展形成的,齒輪中,把一條直線在一個圓上做純滾動,則這條直線上的一個定點的軌跡稱為齒輪的漸開線(即齒輪輪廓線),那么這個圓就叫齒輪的基圓。...
1.節圓螺旋角β:在節圓柱上輪齒齒長曲線和軸線間所成的角度。斜齒齒條的螺旋角,是在節平面上軸向平面和切平面間的交角。除特別指明的以外,螺旋角都是指在...
由一對擺線齒輪組成的齒輪傳動。擺線齒輪的齒廓由內擺線或外擺線組成 (圖中)。滾圓S 在節圓OJ1外面滾動形成齒頂曲線bc,在節圓OJ2內面滾動形成齒根曲線aa′;...
10 節圓直徑 PCD顆粒電荷測定儀 編輯 即Particle Charge Detector,利用流動電勢法,結合標準滴定液滴定的方法來檢測顆粒表面電荷密度的儀器,主要用於造紙、水處理等...
