樹狀圖,亦稱樹枝狀圖。樹形圖是數據樹的圖形表示形式,以父子層次結構來組織對象。是枚舉法的一種表達方式。樹狀圖也是國中學生學習機率問題所需要畫的一種圖形。
基本介紹
- 中文名:樹狀圖
- 外文名: dendrogram
- 相互關係:具有二次元和三次元
- 表達方式:枚舉法
定義,畫法,例題,
定義
為了用圖表示親緣關係,把分類單位擺在圖上樹枝頂部,根據分枝可以表示其相互關係,具有二次元和三次元。在數量分類學上用於表型分類的樹狀圖,稱為表型樹狀圖(phenogram),摻入系統的推論的稱為系統樹狀圖(cladogram)以資區別。表型樹狀圖是根據群析描繪的,系統樹狀圖是根據一種模擬的假定的性狀進化方向即用電子計算機描繪的。
樹狀圖也是國中學生學習機率問題所需要畫的一種圖形。
畫法
最小樹形圖,就是給有向帶權圖中指定一個特殊的點v,求一棵有向生成樹T,使得該有向樹的根為v,並且T中所有邊的總權值最小。最小樹形圖的第一個算法是1965年朱永津和劉振宏提出的複雜度為O(VE)的算法。
判斷是否存在樹形圖的方法很簡單,只需要以v為根作一次圖的遍歷就可以了,所以下面的算法中不再考慮樹形圖不存在的情況。
在所有操作開始之前,我們需要把圖中所有的自環全都清除。很明顯,自環是不可能在任何一個樹形圖上的。只有進行了這步操作,總算法複雜度才真正能保證是O(VE)。
首先為除根之外的每個點選定一條入邊,這條入邊一定要是所有入邊中最小的。現在所有的最小入邊都選擇出來了,如果這個入邊集不存在有向環的話,我們可以 證明這個集合就是該圖的最小樹形圖。這個證明並不是很難。如果存在有向環的話,我們就要將這個有向環所稱一個人工頂點,同時改變圖中邊的權。假設某點u在 該環上,並設這個環中指向u的邊權是in[u],那么對於每條從u出發的邊(u, i, w),在新圖中連線(new, i, w)的邊,其中new為新加的人工頂點; 對於每條進入u的邊(i, u, w),在新圖中建立邊(i, new, w-in[u])的邊。為什麼入邊的權要減去in[u],這個後面會解釋,在這裡先給出算法的步驟。然後可以證明,新圖中最小樹形圖的權加上舊圖中被收縮 的那個環的權和,就是原圖中最小樹形圖的權。
上面結論也不做證明了。現在依據上面的結論,說明一下為什麼出邊的權不變,入邊的權要減去in [u]。對於新圖中的最小樹形圖T,設指向人工節點的邊為e。將人工節點展開以後,e指向了一個環。假設原先e是指向u的,這個時候我們將環上指向u的邊 in[u]刪除,這樣就得到了原圖中的一個樹形圖。我們會發現,如果新圖中e的權w'(e)是原圖中e的權w(e)減去in[u]權的話,那么在我們刪除 掉in[u],並且將e恢復為原圖狀態的時候,這個樹形圖的權仍然是新圖樹形圖的權加環的權,而這個權值正是最小樹形圖的權值。所以在展開節點之後,我們 得到的仍然是最小樹形圖。逐步展開所有的人工節點,就會得到初始圖的最小樹形圖了。
如果實現得很聰明的話,可以達到找最小入邊O(E),找環 O(V),收縮O(E),其中在找環O(V)這裡需要一點技巧。這樣每次收縮的複雜度是O(E),然後最多會收縮幾次呢?由於我們一開始已經拿掉了所有的 自環,我門可以知道每個環至少包含2個點,收縮成1個點之後,總點數減少了至少1。當整個圖收縮到只有1個點的時候,最小樹形圖就不不用求了。所以我們最 多只會進行V-1次的收縮,所以總得複雜度自然是O(VE)了。由此可見,如果一開始不除去自環的話,理論複雜度會和自環的數目有關。
判斷是否存在樹形圖的方法很簡單,只需要以v為根作一次圖的遍歷就可以了,所以下面的算法中不再考慮樹形圖不存在的情況。
在所有操作開始之前,我們需要把圖中所有的自環全都清除。很明顯,自環是不可能在任何一個樹形圖上的。只有進行了這步操作,總算法複雜度才真正能保證是O(VE)。
首先為除根之外的每個點選定一條入邊,這條入邊一定要是所有入邊中最小的。現在所有的最小入邊都選擇出來了,如果這個入邊集不存在有向環的話,我們可以 證明這個集合就是該圖的最小樹形圖。這個證明並不是很難。如果存在有向環的話,我們就要將這個有向環所稱一個人工頂點,同時改變圖中邊的權。假設某點u在 該環上,並設這個環中指向u的邊權是in[u],那么對於每條從u出發的邊(u, i, w),在新圖中連線(new, i, w)的邊,其中new為新加的人工頂點; 對於每條進入u的邊(i, u, w),在新圖中建立邊(i, new, w-in[u])的邊。為什麼入邊的權要減去in[u],這個後面會解釋,在這裡先給出算法的步驟。然後可以證明,新圖中最小樹形圖的權加上舊圖中被收縮 的那個環的權和,就是原圖中最小樹形圖的權。
上面結論也不做證明了。現在依據上面的結論,說明一下為什麼出邊的權不變,入邊的權要減去in [u]。對於新圖中的最小樹形圖T,設指向人工節點的邊為e。將人工節點展開以後,e指向了一個環。假設原先e是指向u的,這個時候我們將環上指向u的邊 in[u]刪除,這樣就得到了原圖中的一個樹形圖。我們會發現,如果新圖中e的權w'(e)是原圖中e的權w(e)減去in[u]權的話,那么在我們刪除 掉in[u],並且將e恢復為原圖狀態的時候,這個樹形圖的權仍然是新圖樹形圖的權加環的權,而這個權值正是最小樹形圖的權值。所以在展開節點之後,我們 得到的仍然是最小樹形圖。逐步展開所有的人工節點,就會得到初始圖的最小樹形圖了。
如果實現得很聰明的話,可以達到找最小入邊O(E),找環 O(V),收縮O(E),其中在找環O(V)這裡需要一點技巧。這樣每次收縮的複雜度是O(E),然後最多會收縮幾次呢?由於我們一開始已經拿掉了所有的 自環,我門可以知道每個環至少包含2個點,收縮成1個點之後,總點數減少了至少1。當整個圖收縮到只有1個點的時候,最小樹形圖就不不用求了。所以我們最 多只會進行V-1次的收縮,所以總得複雜度自然是O(VE)了。由此可見,如果一開始不除去自環的話,理論複雜度會和自環的數目有關。
例題
例1、隨機擲兩枚質地均勻的正方體骰子,骰子的六個面上分別刻有1到6的點數,則這兩個骰子向上的一麵點數都是奇數的機率為多少?
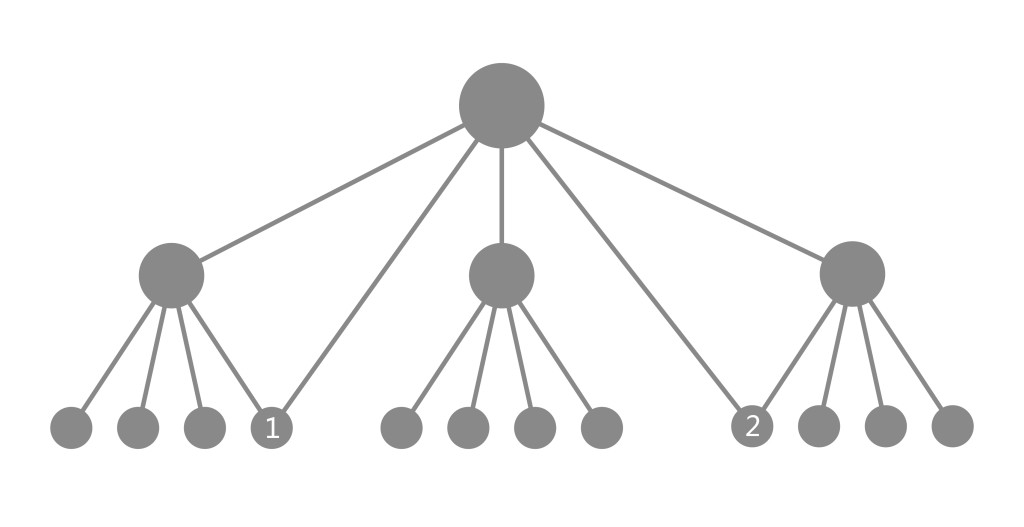
分析:本題中的事件是擲兩枚骰子,看向上的一麵點數,由此可確定本事件包括兩個環節,擲第一枚骰子和擲第二枚骰子,所以樹狀圖該畫兩層。第一枚骰子向上的一面的點數可能是1,2,3,4,5,6等6個的一個,所以第一層應畫6個分叉;再看第二層,第二枚骰子,向上一面的點數可能是6個的一個,所以第二層應接在第一層的6個分叉上,每個小分支上,再有6個分叉。畫出樹狀圖,這樣共得到6×6種情況,從中找出兩個骰子向上的一麵點數都是奇數的情況,再求出機率。
解:畫出樹狀圖,如圖1。

由圖中可以看出,兩枚骰子向上的一麵點數的可能性情況共36種,其中向上的一麵點數都是奇數的情況有(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1)(5,3)(5,5)共9種情況,從而得兩個骰子向上的一麵點數都是奇數的機率(記為事件A)為P(A)=9/36=1/4
點評:由本例看出,只要畫好了樹狀圖,就很容易求出機率。而畫樹狀圖的關鍵一是確定層數,二是確定每層分叉的個數。
例2、一個口袋中裝有紅、白、綠三隻小球,另一隻口袋中裝有(除顏色外其餘都相同)紅、白兩隻小球。現從兩隻口袋中各取一隻小球,求兩隻小球顏色一樣的機率是多少?
分析:本題從兩隻口袋中各取一隻小球,由此可見事件的環節共兩個,樹狀圖畫兩層。由於一隻口袋中裝有三隻小球,所以此層應有三個分叉。另一隻口袋中裝有兩隻小球,拿一個球的可能性有兩種,此層可能有兩個分叉。各層的分叉要畫對。至於兩隻口袋中哪只放上,哪只放下,可以隨便畫,不影響結果。
解:畫出樹狀圖如下圖2(圖3也正確):
從圖中可以看出,兩隻小球顏色的可能性共6種,而兩隻小球顏色一樣的可能性只有(紅,紅),(白,白)共2種,所以兩隻小球顏色一樣的機率(記為事件A)為P(A)=2/6=1/3

點評:本題與上題不同的是兩個口袋的球數不等,所以各層的分叉要根據本層的可能情來確定,這是畫樹狀圖最不易掌握的知識點,大家要多加揣摩。