雅各布第一 生平
雅各布第一1654年12月27生於
巴塞爾 ,1705年8月16日卒於同地。他分別於1671和1676年獲得藝術碩士和神學碩士學位,但他對數學有著濃厚的興趣,他的數學幾乎是無師自通的。1676年,他到
荷蘭 、
英國 、
德國 、
法國 等地旅行,結識了萊布尼茨、惠更斯等著名科學家,從此與萊布尼茨一直保持經常的通訊聯繫,互相探討微積分的有關問題。1687回國後,雅各布第一擔任巴塞爾大學數學教授,教授實驗物理和數學,直至去世。由於雅各布第一傑出的科學成就,1699年,他當選為巴黎科學院外籍院士;1701年被柏林科學協會(後為柏林科學院)接納為會員。
雅各布第一在機率論、微分方程、無窮級數求和、變分方法、解析幾何等方面均有很大建樹。許多數學成果與他的名字相聯繫。例如懸鏈線問題(1690年),曲率半徑公式(1694年),“伯努利雙紐線”(1694年),“伯努利微分方程”(1695年),“等周問題”(1700年),“伯努利數”、“伯努利大數定理”等。雅各布第一對數學最重大的貢獻是機率論。他從1685年起發表關於賭博遊戲中輸贏次數問題的論文,後來寫成巨著《猜度術》,這本書在他死後8年,即1713年才得以出版.他研究了柔鏈、薄片、風帆等在自重作用下的形狀。1694年他指出拉伸試驗中伸長量與拉伸力的m次幕成比例,m由實驗確定。1729年C. D. 比爾芬格(1693〜1750)根據雅各布第一1687年的實驗數據給出m為3/2。雅各布第一在1705年研究過細桿在軸向力作用下的彈性曲線問題。
軼事
最為人們津津樂道的軼事之一,是雅各布痴心於研究對數螺線,他發現,對數螺線經過各種變換後仍然是對數螺線:如它的漸屈線和漸伸線是對數螺線,自極點至切線的垂足的軌跡,以極點為發光點經對數螺線反射後得到的反射線,以及與所有這些反射線相切的曲線(回光線)都是對數螺線。他驚嘆這種曲線的神奇,竟在遺囑里要求後人將對數螺線刻在自己的墓碑上,並附以頌詞“縱然變化,依然故我”,用以象徵死後永生不朽。
約翰第一 約翰第一,1667年8月6日生於巴塞爾,1748年1月1日卒於同地。雅各布第一之弟。最初學醫,同時研習數學。約翰第一於1690年獲醫學碩士學位,1694年又獲得博士學位,其論文是關於肌肉的收縮問題。但他發現他骨子裡的興趣是數學,不久他愛上了微積分。1695年,28歲的他取得了他的第一個學術職位——荷蘭格羅寧根大學數學教授。10年後的1705年,約翰第一接替去世的雅各布第一接任巴塞爾大學數學教授。同他的哥哥一樣,他也當選為巴黎科學院外籍院士和柏林科學協會會員。1712、1724和1725年,他還分別當選為英國皇家學會、義大利波倫亞科學院和彼得堡科學院的外籍院士。
約翰第一是一位多產的數學家,他的大量論文涉及到曲線的求長、曲面的求積、等周問題和微分方程。指數運算也是他發明的。例如解決懸鏈線問題(1691年),提出洛必塔法則(1694年)、最速降線(1696年)和測地線問題(1697年),給出求積分的變數替換法(1699年),研究弦振動問題(1727年),出版《積分學數學講義》(1742年)等。
約翰第一曾對其兄雅各布第一關於懸鏈線(即柔鏈在自重作用下的平衡曲線)作過解釋。1696年提出尋求能使質點從一巳知點最快到達另一已知點的曲線問題,並給出這個問題的解,稱所得曲線為“最速降線”。1728年他在研究弦的振動中已知道基本振型是正弦型的,但還不知道高階振型的性質,1742年研究過雙重擺(擺下掛一擺〉大幅度擺動的微分方程。他一生中與同代科學家一百多人通信達兩千多次,討論了各種學術問題,著有《水力學》(1734)一書。
值得一提的是,1696年約翰第一以公信的方式,向全歐數學家提出了著名的“
最速降線問題 ”,從而引發了歐洲數學界的一場論戰。爭論無疑促進了科學的發展,論戰的結果產生了一個新的數學分支——變分法。因此,約翰第一是公認的變分法奠基人。
約翰第一的另一大功績是培養了一大批出色的數學家,其中包括18世紀最著名的數學家歐拉、瑞士數學家克萊姆、法國數學家洛必塔,以及他自己的兒子丹尼爾和侄子尼古拉二世等。
丹尼爾第一 歷史
丹尼爾第一,1700年2月9日生於荷蘭格羅寧根,1782年3月17日卒於巴塞爾。約翰第一次子。也像其父一樣先習醫,1721年獲巴塞爾大學醫學博士學位,但在其家族的薰陶感染下,不久便轉向數學,在父兄指導下從事數學研究,並且成為這個家族中成就最大者。1724年,他在威尼斯旅途中發表《數學練習》,引起學術界關注,並被邀請到俄國聖彼得堡科學院工作。同年,他還用變數分離法解決了微分方程中的“里卡蒂”方程。第二年,25歲的丹尼爾第一受聘為聖彼得堡科學院數學教授,並被選為該院名譽院士。1733年,他返回巴塞爾,教授解剖學和植物學和自然哲學。丹尼爾第一的貢獻集中在微分方程、機率和數學物理,被譽之為數學物理方程的開拓者和奠基人。他曾10次獲得法國科學院頒發的獎金,能與之相媲美的只有大數學家歐拉。丹尼爾第一於1747年當選為柏林科學院院士,1748年當選巴黎科學院院士,1750年當選英國皇家學會會員。他一生獲得多項榮譽稱號。
成就
作為伯努利家族博學廣識的代表,他的成就涉及多個科學領域。他出版了經典著作《流體動力學》(1738年),給出“伯努利定理”等流體動力學的基礎理論;研究彈性弦的橫向振動問題(1741~1743年),提出聲音在空氣中的傳播規律(1762年)。他的論著還涉及天文學(1734年)、地球引力(1728年)、湖汐(1740年)、磁學(1743、1746年),振動理論(1747年)、船體航行的穩定(1753、1757年)和生理學(1721、1728年)等。
丹尼爾第一以《水動力學,關於流體中力和運動的說明》(1738)一書著稱於世,書中提出流體力學的一個重要定理,反映了理想流體(不可壓縮、不計粘性的流體)中能量守恆定律,這個定理和相應的公式後稱為伯努利定理和伯努利公式。丹尼爾第一的固體力學論著很多。他對好友歐拉提出具體建議,使歐拉解出彈性壓桿失穩後的形狀,即獲得彈性曲線的精確結果。1733~1734年他和歐拉在研究上端懸掛的重鏈的振動問題中用了貝塞爾函式,並在由若干個重質點串連成的離散模型的相應振動問題中引用了拉蓋爾多項式。他在1735年獲得懸臂樑振動方程。1742年提出彈性振動理論中的疊加原理,並用具體的振動實驗進行驗證,他還考慮過不對稱浮體在液面上的晃動方程。
相關傳說
伯努利家族曾產生許多傳奇和軼事。一個關於丹尼爾第一的傳說這是樣的:有一次在旅途中,年輕的丹尼爾第一同一個風趣的陌生人閒談,他謙虛地自我介紹說:“我是
丹尼爾·伯努利 。”陌生人立即帶著譏諷的神情回答道:“那我就是伊薩克·牛頓。”作為丹尼爾第一,這是他有生以來受到過的最誠懇的讚頌,這使他一直到晚年都甚感欣慰。
其他 伯努利家族 丹尼爾第一之弟約翰第二(1710〜1790)在1736年把光看作彈性介質中的壓力波,導得微分方程並用級數求出它的解。他的兒子雅各布第二(1759〜1789)在研究板的彎曲時把板當作兩組互相正交的梁,並認為導出的四階偏微分方程是近似的,只是作為解板問題的一種初步嘗試予以發表(1789)。
伯努利家族星光閃耀、人才濟濟的現象,數百年來一直受到人們的讚頌,也給人們一個深刻的啟示:家庭的“優勢積累”,可以是優秀人才成長的搖籃.
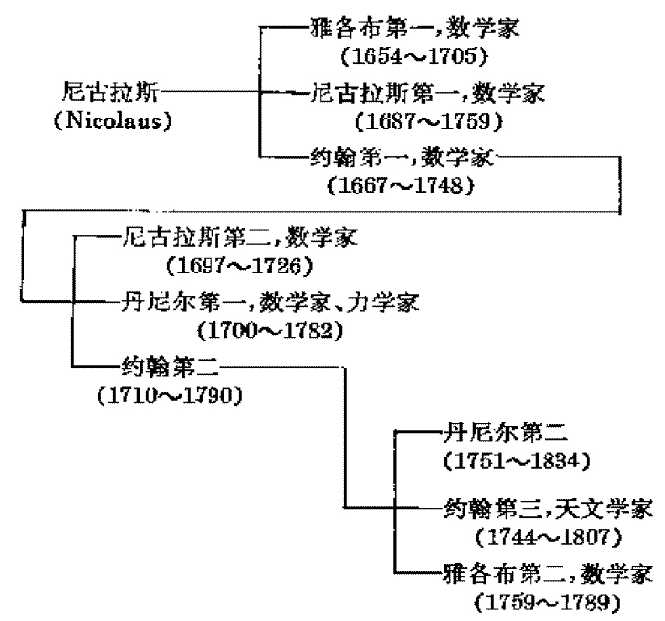 伯努利家族
伯努利家族
