基本介紹
簡介,相關舉例,帆船原理,氣球飛機,船吸現象,颳風,香蕉球,喝水,火車站站台安全線,發現者,流體方程,
簡介
伯努利效應(Bernoulli’s Principle)
比如,管道內有一穩定流動的流體,在管道不同截面處的豎直開口細管內的液柱的高度不同,表明在穩定流動中,流速大的地方壓強小,流速小的地方壓強大。這一現象稱為“伯努利效應”。伯努利方程:p+1/2ρv^2+ρgh=常量(其中,p為壓強,ρ為流體密度,v為流體速度,g為重力加速度,h為高度。)。 兩紙片內側氣流速度快,壓強減小,形成內外側壓力差,使紙片靠攏
兩紙片內側氣流速度快,壓強減小,形成內外側壓力差,使紙片靠攏
 兩紙片內側氣流速度快,壓強減小,形成內外側壓力差,使紙片靠攏
兩紙片內側氣流速度快,壓強減小,形成內外側壓力差,使紙片靠攏在列車站台上都劃有安全線。這是由於列車高速駛來時,靠近列車車廂的空氣將被帶動而運動起來,壓強就減小,站台上的旅客若離列車過近,旅客身體前後出現明顯壓強差,將使旅客被吸向列車而受傷害。
相關舉例
桌球的上旋
鄧亞萍和她的隊友喬紅在第43屆世乒賽上的一場爭奪戰,真可謂是速度和力量的化身。她們兇猛地抽殺推擋,把個小球變成了一道道銀色的電弧,直看得人們眼花繚亂,嘆為觀止。人們可曾知道,在她們不斷加大攻球的速度和力量時,那一個個擊出去的球都帶著上旋?
桌球運動中的攻球,以快速和兇狠給對方造成很大的威脅。但是攻球往往會遇到這樣的尷尬:揮拍過猛,球會不著台面飛出界外;如果因此而不適當地壓低弧線高度,球又會觸網失分。不解決這個準確落點的問題,所謂攻球的威脅也就成了水中月、鏡中花了。那么有沒有一種攻球,可以攜裹著強勁的力量和速度殺向對方,又能縮短打出的距離、增加桌球飛行弧線的高度?有,這就是帶上旋的攻球。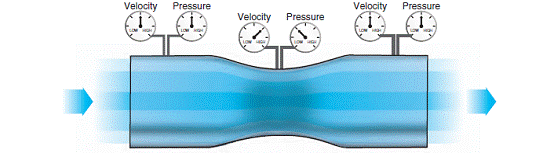 伯努利效應
伯努利效應
 伯努利效應
伯努利效應桌球的上旋,會使球體表面的空氣形成一個環流,環流的方向與球的上旋方向一致。這時,球體還在向前飛行,所以它同時又受到了空氣的阻力。環流在球體上部的方向與空氣阻力相反,在球體下部的方向與空氣阻力一致,所以,球體上部空氣的流速慢,而下部空氣的流速快。流速慢的壓強大,流速快的壓強小,這樣就使球體得到了一個向下的力,這個力又讓球得到了一個加速度。我們把球體向前上方的運動看作是這樣兩個運動的合成:一個是沿水平方向的勻速直線運動,另一個是豎直上拋運動,以此可得出相應的計算式。然後把具體數值代入計算式中,並把計算結果在座標中畫出來,就會聯結出一個具有一定彎曲度的弧線,這就是上旋,能增大桌球飛行弧線的彎曲程度,也就是被運動員用來增加保險係數的弧度。
上旋的利用,使得許多運動員如虎添翼。馬文革在1994年世界明星巡迴賽上速度加旋轉,以2:0輕取1993年世界盃男單冠軍普里莫拉茨,第2局的比分是21:6;在與法國蓋亭爭奪冠軍的決賽中,又以3:1取勝。上旋的特性在弧圈球中表現得最為出色,因為弧圈球的上旋力非常強。法國埃盧瓦凌厲的兩面弧圈技術,使他得以在乒壇上稱霸一方。
帆船原理
人們通常認為帆船只能沿風吹動的方向移動,即順風移動。 但三角帆使帆船還能夠迎著風移動(逆風移動)。 在理解如何逆風移動之前,我們首先需要了解一些與船帆有關的工作原理。
船帆的最先著風之帆緣稱作前緣,它位於船隻的前部. 後部的船翼後緣稱作帆的後緣。 從前緣到帆的後緣的假想水平線稱作弦。船帆的曲度稱作吃水,並且從弦到最大吃水點的垂直距離稱作弦深。 充滿空氣以形成凹面彎曲的船帆的一面稱作迎風面。向外吹以形成凸起形狀的一面稱作背風面。了解了這些術語後,我們將繼續介紹帆船運動。
船隻藉助帆的每一面所產生的力量沿著迎風方向移動。迎風面的正向力量(推力)和背風面的負向力量(拉力)合在一起形成了合力,這兩種力量都作用於同一方向。儘管您可能不認同,但拉力確實是這兩種力量中較強的力量。 伯努利吸啜效應
伯努利吸啜效應
 伯努利吸啜效應
伯努利吸啜效應在1738年,科學家丹尼爾·伯努利發現,氣流速度與周圍自由氣流成比例增加,從而導致壓力的降低,而這可令氣流速度更快。這種情況在帆的背風面發生即空氣流動速度加快並在帆的後面形成低壓區域。
為什麼空氣會加速?空氣與水一樣,都是流動的。當風匯聚並且風被帆分開時,一些風附著在凸起面(背風面)並將帆扯起。為了其上“未附著”的空氣穿過帆,帆必須向不受帆影響的氣流外彎曲。但此類的自由氣流往往保持其直線流動並妨礙航行。自由氣流和彎曲的船帆合在一起形成了一個窄道,起初的氣流必須從中經過。因為它不能自行壓縮,所以空氣必須加速以從該窄道擠過。這就是氣流速度在帆的凸起面增加的原因。
一旦發生這一情況,伯努力的理論就得以生效。窄道中增加的氣流要快於周圍的空氣,並且在氣流速度加快的區域壓力將下降,這就產生了鏈式反應。隨著新的氣流接近最先著風之帆緣並分開,它更多地流向背風面——氣流被吸引到低壓區域並被高壓區域所排斥。現在即使更大塊的空氣也必須更快地擠進凸起帆面和自由氣流形成的窄道,這令空氣壓力更低。這一情況不斷發展直至達到現有風力條件的最大速度,並且在背風面形成最大低壓區域。請注意,只有在氣流達到曲面(弦深)的最深點後氣流才增加。在達到這一點之前,空氣不斷匯聚和加速。超出這一點後,空氣分開並減速,直到再次與周圍空氣速度相當。
在其間,在帆的迎風面發生相反的情況。隨著更多的空氣流過背風面,迎風面上流過帆的凸起面和自由氣流之間的擴展空間的空氣將減少。由於這些氣流四散流動,所以其流速下降到比周圍空氣還低的速度,這導致壓力增加。
在了解了這些潛在的力量之後,我們如何在實際中藉助這些力量來使船隻移動呢? 我們需要在風帆和風之間建立理想的關係,使風不但加速流動,而且可以沿著帆的凸起面流動。船帆和風之間的這一關係的一部分稱作迎角。描繪與風平直的船帆。空氣均勻分開到每一面上 - 船帆下垂而不是充滿成彎曲形狀,空氣沒有加速以在背風面形成低壓區域,並且船隻沒有移動。 但如果船帆與風向剛好成正確角度,則船帆會一下子充滿風並產生空氣動力。
迎角的角度必須十分精確。如果該角度保持與風太近,則船帆的前部將“搶風”或擺動。如果其角度太寬,則沿著帆的曲面流動的氣流將分開並且周圍的空氣重新聚合。這一分離產生了旋轉空氣的“停轉區域”,導致風速下降、壓力增加。因為船帆的曲率將始終導致帆的尾端與風向所成的角度大於與最先著風之帆緣所成角度,所以帆的後緣的空氣不能沿著曲面流動並返回周圍自由空氣的方向。理想上講,在氣流到達帆的後緣前不應開始分離。但隨著船帆的迎角加寬,分離點逐漸前移並將其後的一切保留在停轉區域。
除了迎角保持正確角度以使空氣能夠順利通過外,關於風與帆關係的另一重要因素就是船帆必須具有正確的曲率,以保證空氣始終附著在船尾。如果曲線太小,則氣流將不彎曲,並且將不會產生導致速度增加的壓擠效果。如果曲線太大,則氣流不能被附著。因此,只有在曲率不太大並且迎角不太寬的情況下才能發生分離。
這樣,我們現在就知道風帆壓力是如何在理論上和實際中形成的。但這些壓力是如何令船隻前行的呢? 讓我們更深入地了解其中的奧妙。
在海平面上,每平方米的氣壓是 10 噸。當船帆的背風面上的氣流增強時,您從上文可以知道氣壓將下降。假定每平方米將下降 20 千克。同樣,迎風面上的氣壓將增加 - 假定每平方米增加 10 千克(請記住,下拉壓力強於推送壓力)。並且即使背風壓力是負向並且迎風壓力是正向的,它們都作用於同一方向。因此現在我們每平方米約有共 30 千克的壓力。將其乘以 10 平方米風帆大小,我們在該風帆上已產生了共 300 千克的合力。
船帆上的每一點都作用了不同的壓力。壓力最強處位於弦深處,即船帆曲面最深處。這也是氣流最快和壓力下降最大的地方。隨著氣流向後移動並分離,力量也隨之減弱,這些力量的方向也會更改。在船帆的每一點上,該力量與帆面保持垂直。船帆前部的力量最強處也在最前方向上。在船帆的中部,力量更改為側方向,或傾斜方向。在船帆的後部,隨著風速的下降力量也逐漸減弱,並導致向後方向或往後拉的方向。
船帆各處上的壓力都可以計算出來,以便確定其每一面上前部、後部和牽引部位的相對力量。因為向前的力量還是最強的,所以施加在船帆上的合力還稍偏向前的,但主要是側方向。增加船帆作用以獲得更多向前的驅動力還導致側向力的更大的增加。因此,當風施加在側面的力量達到最大時,船隻是如何前行的呢? 這涉及船帆與風的迎角,還涉及船隻與水的阻力問題。
合力的方向與帆弦近乎垂直。當帆弦與船隻的中線平行時,主要力量幾乎完全施加在側面。但是,如果船帆成一點兒角度,以便船帆產生的力量稍微向前,則船隻本身會立即前行。這是為什麼呢? 船的中線(即龍骨)作用於水的方式類似於船帆作用於風的方式。龍骨產生的力量與船帆傾斜力相反的力量 - 它使船完全保持船帆形成的力量的方向。並且儘管風帆合力始終作用於迎風的那面,但正確的迎角將使船隻前行。
船帆的角度距離船體中線越遠,著力點施加於正面相對於施加於側面的數量越多。將正向力量的稍微調整與水相對於空氣的反向力量結合起來,我們將令船隻迎風前行,因為現在水流的阻力最小。
氣球飛機
氣球有熱氣球和充有氫氣(或氦氣)的氣球,它們都是利用氣球平均密度小於大氣密度在大氣中上浮。跟液體中物體上浮的不同,是高空大氣稀薄,也就是密度較小,大氣壓也小,氣球會向外膨脹。到整個氣球的平均密度跟外面大氣的密度相等的時候,氣球不會再上升。為了氣球繼續上升,辦法是減小氣球的質量,具體方法是將氣球下面攜帶的沙袋丟掉一些。 伯努利效應
伯努利效應
 伯努利效應
伯努利效應將氣球里的氣體放掉一些,體積減小,平均密度增大,氣球就下降。
飛機也能夠上天,但原理與氣球不一樣。比較一下,氫氣球如果不用繩拉著,就會因為浮力大於重力則自己上升。飛機在停機坪上要不要用繩子拉著?
船吸現象
1911年9月20日,“奧林匹克”號正在大海上航行,在距離這艘當時世界上最大遠洋輪的100米處,有一艘比它小得多的英國皇家海軍鐵甲巡洋艦“豪克”號正在向前疾駛,兩艘船似乎在比賽,彼此靠得較攏,平行著駛向前方。忽然,正在疾駛中的“豪克”號好像被大船吸引似地,一點也不服從舵手的操縱,竟一頭向“奧林匹克”號闖去。最後,“豪克”號的船頭撞在“奧林匹克”號的船舷上,撞出個大洞,釀成一件海難事故。
究竟是什麼原因造成了這次意外的船禍?在當時,誰也說不上來,據說海事法庭在處理這件奇案時,也只得糊裡糊塗地判處船長制度不當呢!
後來,人們才算明白了,這次海面上的飛來橫禍,是伯努利原理的現象。我們知道,根據流體力學的伯努利原理,流體的壓強與它的流速有關,流速越大,壓強越小;反之亦然。用這個原理來審視這次事故,就不難找出事故的原因了。原來,當兩艘船平行著向前航行時,在兩艘船中間的水比外側的水流得快,中間水對兩船內側的壓強,也就比外側對兩船外側的壓強要小。於是,在外側水的壓力作用下,兩船漸漸靠近,最後相撞。又由於“豪克”號較小,在同樣大小壓力的作用下,它向兩船中間靠攏時速度要快的多,因此,造成了“豪克”號撞擊“奧林匹克”號的事故。現在航海上把這種現象稱為“船吸現象”。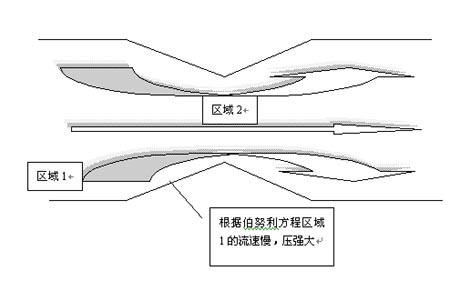 伯努利效應
伯努利效應
 伯努利效應
伯努利效應鑒於這類海難事故不斷發生,而且輪船和軍艦越造越大,一旦發生撞船事故,它們的危害性也越大,因此,世界海事組織對這種情況下航海規則都作了嚴格的規定,它們包括兩船同向行駛時,彼此必須保持多大的間隔,在通過狹窄地段時,小船與大船彼此應作怎樣的規避,等等。
颳風
同樣道理,當颳風時,屋面上的空氣流動得很快,等於風速,而屋面下的空氣幾乎是不流動的。根據伯努利原理,這時屋面下空氣的壓力大於屋面上的氣壓。要是風越刮越大,則屋面上下的壓力差也越來越大。一旦風速超過一定程度,這個壓力差就“嘩”的一下掀起屋頂的茅草,使其七零八落地隨風飄揚。正如我國唐朝著名詩人杜甫《茅屋為秋風所破歌》所說的那樣:“八月秋高風怒號,卷我屋上三重茅。”
你現在明白了吧,為什麼到水流湍急的江河裡去游泳是很危險的事。有人計算了一下,當江心的水流以每秒1米的速度前進時,差不多有30公斤的力在吸引著人的身體,就是水性很好的游泳能手也望而生畏,不敢隨便游近吶!
香蕉球
如果你經常觀看足球比賽的話,一定見過罰前場直接自由球。這時候,通常是防守方五六個球員在球門前組成一道“人牆”,擋住進球路線。進攻方的主罰隊員,起腳一記勁射,球繞過了“人牆”,眼看要偏離球門飛出,卻又沿弧線拐過彎來直進球門,讓守門員措手不及,眼睜睜地看著球進了大門。這就是頗為神奇的“香蕉球”。
桌球中,運動員在削球或拉弧圈球時,球的線路會改變,道理與“香蕉球”一樣。
喝水
人喝水時,同樣套用到伯努利效應。當你把杯子舉到口邊時,你的嘴會習慣地去“吸”杯中的水。這時,胸部擴大,肺里和嘴裡的氣體壓強減小,嘴附近的空氣就向嘴裡跑。並且越靠近嘴的空氣跑的(流動)的越快,對水面的壓強也就越小。於是對於杯里的水面來說,近嘴部分受到空氣的壓強小,較遠部分則大,在不等的壓強作用下,近嘴部分的水面就稍微高了一點起來,超過杯沿流到口內。(摘自《故事物理學》,劉仁隆編著,科學出版社1980年版,略有修改)
火車站站台安全線
火車站站台上,離站台邊緣1米左右的地方都會標有一條安全線,候車時乘客必須在安全線後,這就是防止“伯努利效應”造成危害。
根據“伯努利效應”,流體流動速度加快,它們對旁側的壓力就會減小。火車高速駛過,會對站在它旁邊的人產生很大的力把人“推”向火車。曾有人測算過,當火車以50 km/h 的速度駛過時,產生的力相當於用 78 牛的力把人從背後“推”向火車。
發現者
丹尼爾·伯努利(Daniel Bernoulli)是著名的伯努利家族中最傑出的一位,他是約翰·伯努利(Johann Bernoulli)的第二個兒子。丹尼爾出生時,他的父親約翰正在格羅寧根擔任數學教授。1713年丹尼爾開始學習哲學和邏輯學,並在1715年獲得學士學位,1716年獲得藝術碩士學位。在這期間,他的父親,特別是他的哥哥尼古拉·伯努利第二(Nikolaus Bernoulli II,1695—1726)教他學習數學,使他受到了數學家庭的薰陶。他的父親試圖要他去當商業學徒,謀一個經商的職業,但是這個想法失敗了。於是又讓他學醫,起初在巴塞爾,1718年到了海德堡,1719年到施特拉斯堡,在1720年他又回到了巴塞爾。1721年通過論文答辯,獲得醫學博士學位。他的論文題目是“呼吸的作用”(De respiratione)。同年他申請巴塞爾大學的解剖學和植物學教授,但未成功。1723年,丹尼爾到威尼斯旅行,1724年,他在威尼斯發表了他的《數學練習》(Exercitationes mathematicae),引起許多人的注意,並被邀請到彼得堡科學院工作。1725年,他回到巴塞爾。之後他又與哥哥尼古拉第二一起接受了彼得堡科學院的邀請,到彼得堡科學院工作。在彼得堡的8年間(1725—1733),他被任命為生理學院士和數學院士。1727年,他與L·歐拉(Euler)一起工作,起初歐拉作為丹尼爾的助手,後來接替了丹尼爾的數學院士職位。這期間丹尼爾講授醫學、力學、物理學,做出了許多顯露他富有創造性才能的工作。但是,由於哥哥尼古拉第二的暴死以及嚴酷的天氣等原因,1733年他回到了巴塞爾。在巴塞爾他先任解剖學和植物學教授,1743年成為生理學教授,1750年成為物理學教授,而且在1750—1777年間他還任哲學教授。 1733年,丹尼爾離開彼得堡之後,就開始了與歐拉之間的最受人稱頌的科學通信,在通信中,丹尼爾向歐拉提供最重要的科學信息,歐拉運用傑出的分析才能和豐富的工作經驗,給以最迅速的幫助,他們先後通信40年,最重要的通信是在1734—1750年間,他們是最親密的朋友,也是競爭的對手。丹尼爾還同C·哥德巴赫(Goldbach)等數學家進行學術通信。
流體方程
理想正壓流體在有勢徹體力作用下作定常運動時,運動方程(即歐拉方程)沿流線積分而得到的表達運動流體機械能守恆的方程。因D·伯努利於1738年提出而得名。對於重力場中的不可壓縮均質流體,方程為p+ρgz+1/2ρv^2=常量,式中p、ρ、v 分別為流體的壓強、密度和速度;z為鉛垂高度;g為重力加速度。 上式各項分別表示單位體積流體的壓力能p、重力勢能ρg z和動能1/2ρv^2 ,在沿流線運動過程中,總和保持不變,即總能量守恆。但各流線之間總能量(即上式中的常量值)可能不同。對於氣體,可忽略重力,方程簡化為 p+1/2ρV^2=常量(p0),各項分別稱為靜壓、動壓和總壓。顯然 ,流動中速度增大,壓強就減小;速度減小, 壓強就增大;速度降為零,壓強就達到最大(理論上應等於總壓)。飛機機翼產生舉力,就在於下翼面速度低而壓強大,上翼面速度高而壓強小,因而合力向上。 據此方程,測量流體的總壓、靜壓即可求得速度,成為皮托管測速的原理。在無旋流動中,也可利用無旋條件積分歐拉方程而得到相同的結果但涵義不同,此時公式中的常量在全流場不變,表示各流線上流體有相同的總能量,方程適用於全流場任意兩點之間。在粘性流動中,粘性摩擦力消耗機械能而產生熱,機械能不守恆,推廣使用伯努利方程時,應加進機械能損失項。

