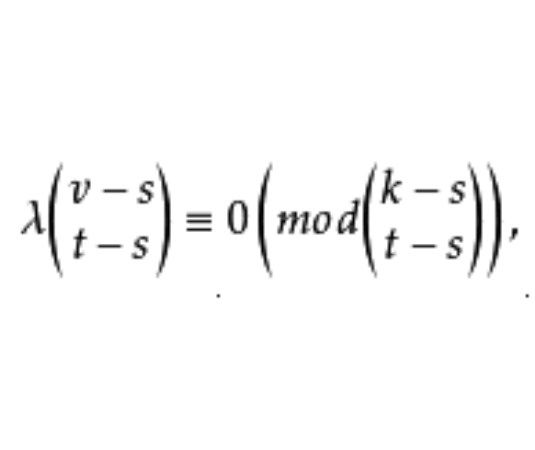t設計大集

t設計大集(large set of t-designs)是一類組合構形，指子集族的一種劃分。為避免一些平凡情形， t-(v，k，λ)設計的大集只對極小的λ定義。

基本介紹

• 中文名：t設計大集
• 外文名：large set of t-designs
• 所屬學科：數學
• 所屬問題：組合學（組合設計理論）
• 簡介：子集族的一種劃分

基本介紹

t設計大集指子集族的一種劃分，為避免一些平凡情形， t-(v，k，λ)設計的大集只對極小的λ定義。當t-(v，k，λ)設計存在時，其參數滿足

s=0，1，…，t-1，設λ*是使上述同餘式成立的最小正整數λ，若v元集X的全體k元子集

可以劃分為互不相交的t-(v，k，λ*)設計的並，則稱這樣的劃分為t-(v，k，λ*)設計的大集，大集中含

個不相交的設計。

發展歷程

最簡單的t設計大集是施泰納三元系大集，其存在問題已最後解決，除不存在STS(7)的大集外，當v≡1，3(mod 6)時STS(v)的大集都存在，STS(v)的大集記為LSTS(v)，共含v-2個不相交STS(v)，凱萊(A.Cayley)於1850年指出：只可能有兩個不相交的STS(7)，因而，不存在LSTS(7)，柯克曼(T.P.Kirkman)於1850年指出：LSTS(15)存在，在隨後的100多年中，雖有多人研究而無大的進展，泰爾林克(L.Teirlink)於1973年證明：LSTS(v)的存在蘊含著LSTS(3v)的存在性，從而，得到LSTS(3)的存在性，隨後，羅薩(A.Rosa)於1975年證明：當LSTS(v)存在時，必存在LSTS(2v+1)，此外，還知道一些v值較小時的LSTS(v)，中國的陸家羲於1983-1984年連續發表的6篇論文，使該問題接近了最後解決，陸家羲為此引進了一類輔助設計，稱為LD設計(參見“LD設計”)，後來，泰爾林克證明了LD設計的PBD閉的性質，從而對陸遺留的6個v值也證明了LSTS(v)的存在性，對其他參數的t設計大集尚缺少一般結果，只對較小的v值有大集存在或不存在的參數表，但未知者甚多，其中參數最小的未知大集為2-(12，4，3)設計的大集，很久以來就有人研究一種特殊的LSTS(v)，即其中每一個STS(v)都是可分解的，雖然LSTS(v)的存在性已徹底解決，但這一類大集問題的結果很少(參見“西爾維斯特問題”)。