伯恩賽德引理（Burnside's lemma），也叫伯恩賽德計數定理（Burnside's counting theorem），柯西-弗羅貝尼烏斯引理（Cauchy-Frobenius lemma）或軌道計數定理（orbit-counting theorem），是群論中一個結果，在考慮對稱的計數中經常很有用。該結論被冠以多個人的名字，其中包括威廉·伯恩賽德（William Burnside）、波利亞、柯西和弗羅貝尼烏斯。這個命題不屬於伯恩賽德自己，他只是在自己的書中《有限群論 On the Theory of Groups of Finite Order》引用了，而將其歸於弗羅貝尼烏斯 (1887)
基本介紹
- 中文名：burnside引理，伯恩賽德引理
- 外文名：Burnside's lemma,Burnside's counting theorem,Cauchy-Frobenius lemma,orbit-counting theorem
- 歸類：組合數學
- 記載：《有限群論》
- 註明：結論並不屬於伯恩賽德
定義,證明,套用,推廣,歷史,
定義
設G={a1,a2,…ag}是目標集[1,n]上的置換群。每個置換都寫成不相交循環的乘積。
是在置換ak的作用下不動點的個數，也就是長度為1的循環的個數。通過上述置換的變換操作後可以相等的元素屬於同一個等價類。若G將[1,n]劃分成l個等價類，則：
等價類個數為：
證明
證明1：
，記
表示g(x) = x否則
。考慮以下和式：
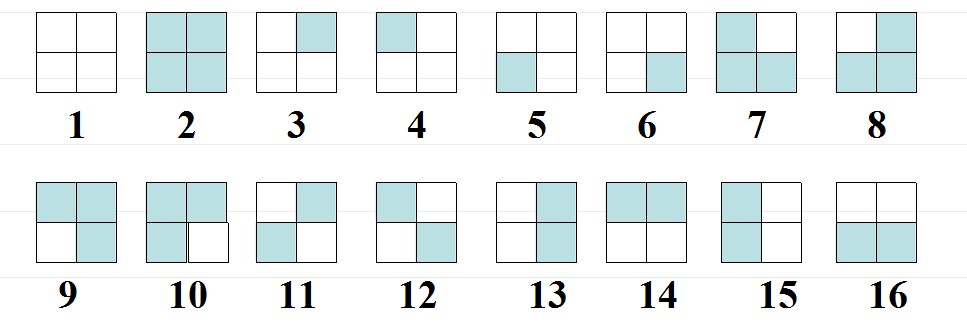
套用
例1：一正方形分成4格，2著色，有多少種方案？其中，經過轉動相同的圖象算同一方案。
解：每個格子一共有兩種顏色可以選擇，所以共有右圖16中圖像。
對圖中圖像的置換可以分為以下四種：
不動：a1=(1)(2)…(16)
逆時針轉90度 ：a2=(1)(2)(3 4 5 6)(7 8 9 10) (11 12)(13 14 15 16)
順時針轉90度 ：a3=(1)(2)(6 5 4 3)(10 9 8 7)(11 12)(16 15 14 13)
轉180度：a4=(1)(2)(3 5)(4 6)(7 9)(8 10)(11)(12) (13 15)(14 16)
由Burnside引理，共有(16+2+2+4)/4=6(種方案)
由例子可見，Burnside引理是針對圖像集的轉動群來求解，當多種顏色(N>2)著色時，理論上可以用Burnside來求解，但是極其複雜，此時一般通過Pólya定理求解。
例2 ：用六種顏色給立方體的六個面著色，每面顏色不同，並且當一個著色的立方體經轉動可得到另一個時，就認為二者相同。問有多少種著色方案？
解：使用六種顏色對立方體的面染色，通過旋轉得到的情形視為同一種方案，最終染
色方式總數可以由這個公式確定。
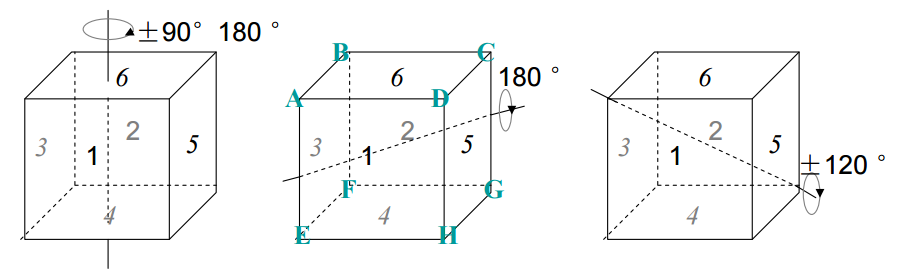
分別選取面心-面心、立方體對角線、棱中-棱中3類共12條軸進行旋轉
旋轉情況 | 置換個數 | 不動點個數 |
不動 | 1×1 | 6！ |
面心-面心旋轉±90° | 3×2 | 0 |
面心-面心旋轉180° | 3×1 | 0 |
棱中-棱中旋轉 | 6×1 | 0 |
立方體對角線旋轉±120° | 4×2 | 0 |
從而有 30 種旋轉不同的立方體 六色染色方式。一般地，使用n種顏色，應當使用Pólya定理求解，此時立方體不同的旋轉面染色數是:
推廣
Burnside引理的權重形式
G是Sn的子群， 數k的權重由函式w給出，一個軌道中的所有數有相同的權重。設G導出的軌道是E1, E2, …, En，每個軌道的權重等於其中一個數的權重。若g∈G，令w'(g)為g所保持不動的所有數權重的和。則有:
證明過程見《Short Proof of a General Weight Burnside Lemma》，
歷史
威廉·伯恩賽德在他1897年關於有限群的書中陳述並證明了這個引理，將其歸於弗羅貝尼烏斯。不過在弗羅貝尼烏斯以前，這個公式在1845年已經為柯西所知。事實上，這個引理明顯如此有名，伯恩賽德不過忽略了將其歸於柯西。因此，這個引理有時候也稱為不是伯恩賽德的引理。這可能看起來不那么有歧義，伯恩賽德對這個領域貢獻了許多引理。
