波利亞定理

Pólya定理是非常重要和基本的計數工具。Pólya定理是匈牙利數學家Pólya利用發生函式的方法，結合群的觀點和權的概念建立起來的一個有關計數定理。Pólya定理在有關計算不同等價類的個數問題上起著重要的作用。

基本介紹

• 中文名：波利亞定理
• 外文名：Pólya theorem
• 提出者：Pólya
• 提出時間：1937
• 套用學科：組合數學 

人物信息

波利亞(1887.12.13-1985.9.7)，美國著名數學家、教育家。1940年移居美國，先在布朗大學任教。1942年後一直在史丹福大學任教。1953年起，任該校退休教授。以他的名字命名的波利亞計數定理則是近代組合數學的重要工具。波利亞還是傑出的數學教育家，他對數學思維一般規律的研究，堪稱是對人類思想寶庫的特殊貢獻。在前人研究同分異構體計數問題的基礎上，波利亞在1937年以「關於群、圖與化學化合物的組合計算方法」為題，發表了長達110頁、在組合數學中具有深遠意義的著名論文．
波利亞的重要數學著作有《怎樣解題》、《不等式》(與哈代、李特伍德合著)、《數學的發現》多卷、《數學與猜想》多卷

背景知識

(1)群(group)的定義 ：給定集合G和G上的二元運算 · ，滿足下列條件稱為群：

(a)封閉性(Closure)：

若a,b∈G，則存在c∈G，使得a·b=c。

(b)結合律(Associativity)：

任意a,b,c∈G，有(a·b)·c=a·(b·c)。

由於結合律成立，(a·b)·c=a·(b·c)可記做a·b·c；

(c)有單位元(Identity)：

存在e∈G，任意a∈G，a·e=e·a=a。

(d)有逆元(Inverse)：

任意a∈G，存在b∈G,，a·b=b·a=e.。記為b=a。

(2)置換群

置換群是最重要的有限群，所有的有限群都可以用之表示。[1,n]到自身的1-1映射稱為n階置換。n階置換共有n!個，同一置換用這樣的表示可有n!個表示法。[1,n]上的由多個置換組成的集合在置換乘法下構成一個群,則稱為置換群，證明如下：

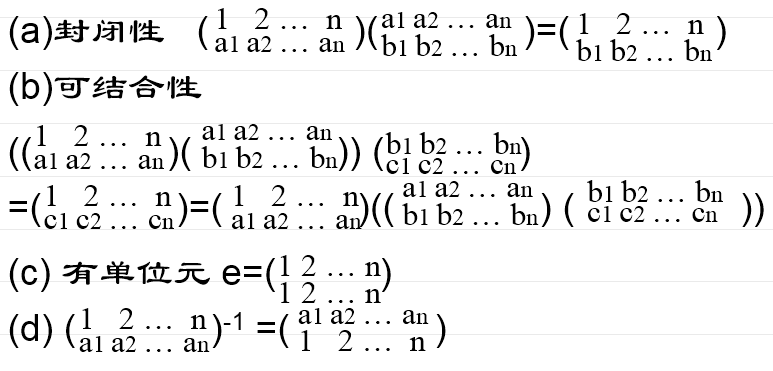
（3）Burnside引理

設G是[1,n]上的一個置換群。G是S_n的一個子群. k∈[1,n]，G中使k元素保持不變的置換全體，稱為k不動置換類，記做Z_k。設G={a₁,a₂,…a_g}是目標集[1,n]上的置換群。每個置換都寫成不相交循環的乘積。c₁(a_k)是在置換a_k的作用下不動點的個數，也就是長度為1的循環的個數。G將[1,n]劃分成l個等價類。等價類個數為：l=

定理概念

設 是n個對象的一個置換群，C(P_k)是置換P_k的循環的個數，用m種顏色對n個對象著色, 著色方案數為：

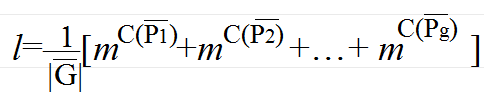
區別

比較Pólya定理和Burnside引理

（1）Pólya定理中的群G是作用在n個對象上的置換群
（2）Burnside引理中的群G是對這n個對象染色後的方案集合上的置換群
（3）兩個群之間的聯繫：群G的元素，相應的在染色方案上也誘導出一個屬於G的置換p

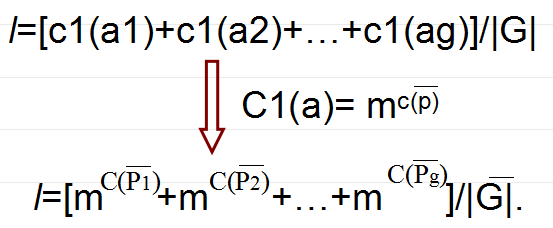
（4）通過Pólya定理和Burnside引理的對比，我們可以看出：在a_i作用下不動的圖象正好對應p_i的循環節中的對象染以相同顏色得到的圖象。C₁(a_i)=m_ii

舉例

1.等邊三角形的3個頂點用紅，藍，綠3著色，有多少種方案？

2.在正6面體的每個面上任意做一條對角線，有多少方案？

解： 在每個面上做一條對角線的方式有2種，可認為是面的2著色問題。但面心-面心的轉動軸轉±90時，無不動圖像象。除此之外，都有不動圖像。正六面體轉動群:面的置換表示

不動: (1)(2)(3)(4)(5)(6) (1) 1個

面面中心轉±90度 (1)(4)2*3個

面面中心轉180度 (1)(2)3個

棱中對棱中轉180度 (2) 6個

對角線為軸轉±120度 (3) 2*4個

正六面體轉動群的階數為24

故方案數為：[26+0+3·24+8·22+6·23]/24=[8+6+4+6]/3=8

母函式型定理

Sk=(b₁+b₂+…+b_m),k=1,2…n

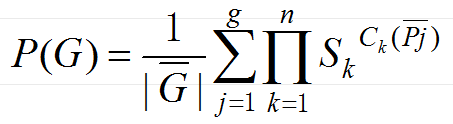
舉例

1.把4個球a,a,b,b放入3個不同的盒子裡,求方案數,若不允許有空盒,有多少分配方案?

解:設這4個球分別為a1,a2,b1,b2,將4個球放入3個盒子,可抽象為對4個球的三著色。

G={e,(a1a2),(b1b2),(a1a2)(b1b2)}

l=(3+2*3+3)/4=36

P(G)=((r+b+g)+2*(r+b+g)(r+b+g)+(r+b+g))/4

展開後取rbg項,i,j,k>0

rbg的係數= rbg的係數= rbg的係數= (C(4,1)*C(3,1)*C(2,2)+2*C(2,1))/4=4
故若不允許有空盒, 分配方案有4*3=12種

2.4顆紅色珠子嵌在正6面體的4個頂點上，有多少方案？

解 ：當於對頂點2著色，無珠設b。

正六面體轉動群：頂點的置換表示

–不動: (1) 1個

–面面中心轉±90度 (4)2*3個

–面面中心轉180度 (2)3個

–棱中對棱中轉180度(2)6個

–對角線為軸轉±120度 (1)(3) 2*4個

–正六面體轉動群的階數為24

–p=[(b+r)+6(b+r) +9(b+r) +8(b+r)(b+r)]/24

方案數：求br的係數 (C(8,4)+12+9*C(4,2)+8*C(2,1)*C(2,1))/24=7

定理的推廣

1. 假定 是作用於 的置換群， 是作用於 的置換群。

若 和 是不相交的兩個集合， ，令 作用於 ，有

換句話說，若用 表示上面的運算，它是作用於 個元素

的置換，它對 的作用屬於 的置換，對 的作用屬於 的置換。這樣的群用 來表示，群 的階應有

現在再來看看 和 、 的關係如何？假如 的格式為

的格式為

則 的格式為

所以

2. 作用於 ，即 作用與 ，使 ， 。同樣有 。

群 的階為 。

若存在 和 ，使得 ，有 。令 則有 ，而且 是使 成立的 的最小值。所以元素 是 中屬於群 的 -循環.這樣的 -循環數目為

對於一般的有：

其中 ， ， ，。