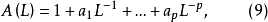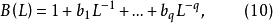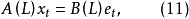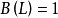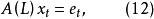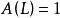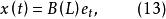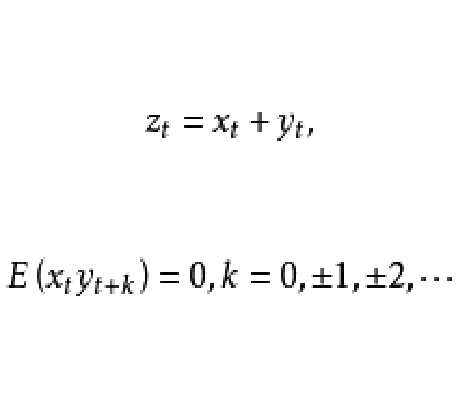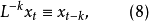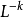數學家Herman Wold(沃爾德)提出平穩隨機過程總可以分解成“可預測”和“純隨機”兩部分之和，這就是Wold分解定理，Wold分解定理是(模型)參數法功率譜估計的思想基礎。
基本介紹
- 中文名：Wold分解定理（沃爾德分解定理）
- 外文名：Wold decomposition theorem
- 提出時間：1938年
- 提出者：Herman Wold
- 相關概念：平穩過程，正則過程，奇異過程等
基本介紹,相關概念,隨機過程的隨機性,奇異過程,正則過程,實際過程,
基本介紹
數學家Herman Wold( 沃爾德1902-1950)1938年提出：任何一個平穩過程都可以分解為兩個不相關(或是說相互正交)的平穩過程之和。其中一個為確定性部分，可以用過去值描述現在值的部分，也稱為可預測部分(或奇異部分)；另一個為純隨機性部分，也稱為正則部分。
設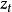
為平穩隨機過程，
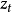總可以分解為
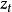
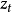
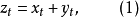
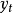
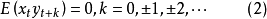
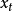
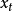
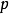
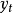
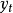
平穩隨機過程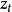
總可以表示成(7)式所示的自回歸-滑動平均方程。Wold將平穩過程分解為奇異和正則兩部分，奇異部分是可以精確預測部分，正則部分是無法準確預測部分。Wold分解定理是一種存在性的結論。並且，分解是在最優線性預測意義下定義的，對一般性的最優估計不適用。另外，Wold 分解沒有給出預測誤差的界，也沒有指明求解隨機過程結構參數的方法。
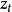
相關概念
隨機過程的隨機性
隨機性是隨機過程的最根本特徵。但是，事物總有兩面性，隨機過程也不例外。可以說,隨機過程是隨機性與確定性的矛盾統一體。隨機變數的隨機性表現在無法用確定函式描述其樣本函式，確定性表現在其統計特徵可以用確定函式(或值)描述。隨機過程是隨機變數隨時間的推演，所以隨機過程的隨機性與確定性表現為隨機變數的隨機性與確定性隨著時間的推演。隨著時間的推演，一方面不斷有新的隨機變數產生，帶來新的不確定性，另一方面不確定性隨時間的推演可以具有確定的規律性。
根據隨機性隨時間的變化情況，可以將隨機過程分為奇異過程( 可預測過程)和正則過程(不可預測過程)。
奇異過程
如果過程的隨機性不隨時間變化，則稱該過程為奇異過程。要注意的是隨機性不變，不是沒有隨機性，只是隨機性不隨時間改變。按資訊理論的觀點，隨著時間的發展，奇異過程沒有新的隨機因素加入，過程所含信息量保持不變，不再提供任何新信息。按預測的觀點，奇異過程是“可預測”過程。“可預測”的涵義是：用過程的過去值對未來值進行預測時，能夠實現一致性預測，即預測的均方誤差能夠趨於0。在預測方法上，一般考慮線性預測。
對於隨機過程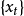
，考慮用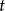
時刻之前的p個值的線性組合對t 時刻的真值
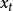進行線性預測:
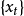
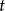
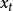
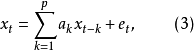
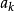
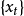
(3)式是一個p階自回歸差分方程。我們將滿足(1)式的隨機過程稱為p階AR過程，記為AR(p)。
正則過程
如果任何兩個不同時刻的隨機性都不相同，則稱該過程為正則過程。正則過程是與奇異過程特徵恰好相反的過程。按資訊理論的觀點，任一時刻的下時刻，正則過程都有新信息加入。按預測的觀點，正則過程是“不可預測”過程。“不可預測”的涵義是無法實現一致性預測，
白噪聲過程是正則過程的代表。對於任何分布的正則過程( 不可預測過程)，總可以用白噪聲過程的線性組合表示，即
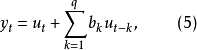
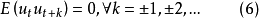
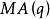
實際過程
奇異過程(可預測過程)和正則過程(純隨機過程)是隨機過程的兩個極端。一般隨機過程的隨機性、可預測性介於奇異過程和正則過程之間。因此，實際隨機過程可以表示為
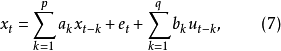
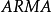
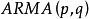
引人移位運算元可以簡化模型差分方程(7)式的表達。定義
