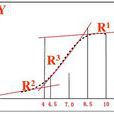
TS（Takagi-Sugeno） 模糊模型由 Takagi 和 Sugeno 兩位學者在 1985 年提出。該模型的主要思想是將非線性系統用許多線段相近的表示出來，即將複雜的非線性問題轉化為在不同小線段上的問題。
基本介紹
- 中文名：TS模糊模型
- 外文名：TS fuzzy model
- 別稱：Takagi-Sugeno模糊模型
- 提出時間：1985年
- 提出者：Takagi 和 Sugeno
- 分類：TS輸入輸出、狀態方程模糊模型
簡介,分類,TS輸入輸出模糊模型,TS狀態方程模糊模型,TS混合模糊模型,TS模型的優點,
簡介
TS 模糊模型是由多個線性系統對同一個非線性系統進行擬合，利用模糊算法進行輸入變數的解構，通過模糊演算推理再去模糊化，生成數條代表每組輸入與輸出關係的方程。
TS模糊模型是由一組If-then模糊規則來描述的非線性系統，每條規則代表一個子系統，其原始形式模糊蘊含條件句形如“If x is M , then y=f(x)”，其中f(x)是x的線性函式。通常情況下f(x)是x的多項式函式，當f(x)是一階多項式時，對應的模糊推論系統稱為一階TS模糊模型；當f是常量時，稱為零階TS模糊模型。
分類
TS模糊模型的規則庫對應了靜態回歸模型y=f(x)，根據回歸變數x選擇的不同，TS模糊模型可以分為輸入輸出形式和狀態方程形式。另外，它還可以和精確模型結合，發展成為混合形式的TS模糊模型。
TS輸入輸出模糊模型
對於離散系統模型，令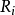
表示模糊系統的第i條規則，其一階TS模糊模型典型的模糊蘊含條件句為：
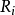
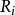
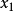
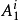
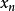
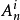
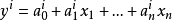
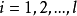
從樣本數據中辨識出的TS模糊模型一般為輸入輸出形式，最常用的形式為非線性自回歸(NARX)模型。
在系統輸入輸出變數的階次己知時，可將上式轉述為：
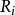
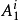
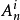
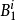
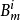
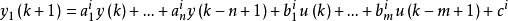
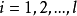
如果可以確定系統參數與輸入變數無關,前件中的輸入變數項也可以去掉。
模糊系統的輸出為各子系統輸出的加權平均，即：
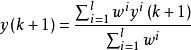
其中模糊化採用單點模糊化，清晰化採用加權平均法。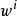
第i條規則的適用度,直積運算採用求積法，即：
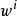
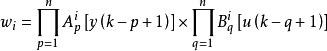
這裡定義符號A(x)為x屬於A的隸屬度，即A(x)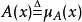
。
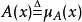
類似地，對於連續系統模型，令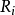 表示模糊系統的第i條規則，其典型的模糊蘊含條件句為：
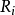
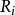
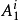
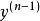
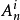
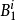
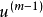
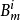
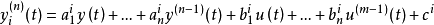
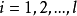
系統的輸出為：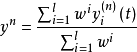
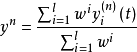
其中，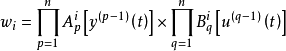
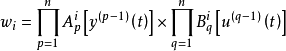
TS狀態方程模糊模型
TS輸入輸出模糊模型對於離散系統可看作模糊差分方程模型，對於連續系統可看作是模糊微分方程模型。很自然地，可以將以上形式推廣到狀態方程情形，建立模糊狀態方程模型。其一般適用在有足夠多的先驗知識來決定系統結構和辨識狀態變數的情況下，它的一個好處就是模型的結構是與實際系統相關的，模型的規則和參數也和實際系統物理相關。
TS混合模糊模型
在許多系統，例如化學和生物化學過程中，建模工作可以分為兩部分：對熟知的機理基於例如質量和能量守恆(第一建模原則)等的建模，和對部分未知的關係的近似例如特殊的反應速率等的建模。後一部分常常涉及到過程在一定假設下才有效的經驗模型的使用。在假設不能達到或過程只是部分已知的時候模型是極不精確的。在這種情況下，基於微分或差分方程的第一原則模型可以和表述啟發式知識經驗的模糊模型結合在一起。這種設定的好處是模糊模型可以提供數字預測和對未知關係的質的判斷。
這種方法的一個例子是Bbauska(1996)提出的抗生素一G酶轉換的動力學方程,酶的轉換由質量守恆方程進行建模，模型描述了化學元素的濃縮和反映物的體積的動態關係，是一個偏分方程。因為轉換速率是變化的,依賴於其它過程變數，由其所描述的轉換過程動力學方程則由TS模糊模型來描述，TS模糊模型來源於過程的測量值和專家的經驗。這樣整個轉換過程是一個確定性模型和一個模糊模型的結合，這是一個典型的TS混合模糊系統模型。
TS模型的優點
(1)具有連續函式的映射能力；
(2) 集成專家控制經驗，以If一Then規則的形式表示，具有知識表達的特點；
(3) 局部線性化動態模型可以用現代控制理論的方法進行系統分析和設計；
(4) 可以根據系統的輸入輸出數據進行辨識，具有定量和定性知識集成的特點；
(5) 可以用較少的模糊規則表示高度非線性的複雜系統。
