基本介紹
- 中文名:均方根誤差
- 外文名:Root Mean Squared Error
- 又稱:標準誤差
- 表達式:√[∑di^2/n]=Re
釋義,定義,舉例,公式,意義,
釋義
均方根誤差是預測值與真實值偏差的平方與觀測次數n比值的平方根,在實際測量中,觀測次數n總是有限的,真值只能用最可信賴(最佳)值來代替。標準誤差 對一組測量中的特大或特小誤差反映非常敏感,所以,標準誤差能夠很好地反映出測量的精密度。這正是標準誤差在工程測量中廣泛被採用的原因。因此,標準差是用來衡量一組數自身的離散程度,而均方根誤差是用來衡量觀測值同真值之間的偏差,它們的研究對象和研究目的不同,但是計算過程類似。
定義
標準差也被稱為標準偏差,或者實驗標準差。
:√[∑di^2/(n-1)]=Re,(式中:n為測量次數);
舉例
比如兩組樣本:
第一組有以下三個樣本:3,4,5
第二組有以下三個樣本:2,4,6
同樣,方差、標準差(方差開根,因為單位不統一)都是表示數據的離散程度的。
公式
S={[(x1-x)^2+(x2-x)^2+......(xn-x)^2]/N}^0.5(x為平均數,N為樣本個數)此公式中的X也就是所謂的平均數應改為x'1,x'2......(即真實值)。均方根誤差算的是觀測值與其真值,或者觀測值與其模擬值之間的偏差,而不是觀測值與其平均值之間的偏差。
意義
它的計算方法是先平方、再平均、然後開方。比如幅度為100V而占空比為0.5的方波信號,如果按平均值計算,它的電壓只有50V,而按均方根值計算則有70.71V。這是為什麼呢?舉一個例子,有一組100伏的電池組,每次供電10分鐘之後停10分鐘,也就是說占空比為一半。如果這組電池帶動的是10Ω電阻,供電的10分鐘產生10A的電流和1000W的功率,停電時電流和功率為零。
PMTS1.0抽油機電能圖測試儀對電流、電壓與功率的測試計算都是按有效值進行的,不會因為電流電壓波形畸變而測不準。這一點對於測試變頻器拖動的電機特別有用。
標準差為了說明樣本的離散程度。
均方根值也稱作為效值。
那么在20分鐘的一個周期內其平均功率為500W,這相當於70.71V的直流電向10Ω電阻供電所產生的功率。而50V直流電壓向10Ω電阻供電只能產生的250W的功率。對於電機與變壓器而言,只要均方根電流不超過額定電流,即使在一定時間內過載,也不會燒壞。均方根誤差為了說明樣本的離散程度。對於N1,....Nm,設N=(N1+...+Nm)/m;則均方根誤差記作:F6F!M n+t8Q5i.Y-m
t=sqrt(((N^2-N1^2)+...+(N^2-Nm^2))/(m(m-1)))。

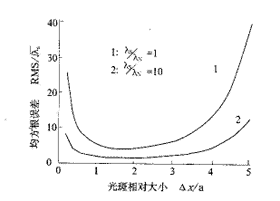 均方根誤差
均方根誤差