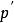NOT運算

在邏輯中，NOT運算是一種操作，它將命題P帶到另一個命題“非P”，寫為¬P，當P為假時直觀地解釋為真，而當P為真時則為假。 因此，否定是一元（單一論證）邏輯連詞。 它可以更普遍地用作對概念，命題，真值或語義值的操作。 在經典邏輯中，否定通常用真值函式來識別，該真值函式將真值用於虛假，反之亦然。 在直覺主義邏輯中，根據Brouwer-Heyting-Kolmogorov解釋，命題P的否定是其證明是P的反駁的命題。

基本介紹

• 中文名：NOT運算
• 外文名：Negation

定義

關於否定性的可能性，關於其邏輯地位，功能和意義，關於其適用範圍......以及對否定判斷的解釋，沒有達成協定。

經典否定是對一個邏輯值的操作，通常是命題的值，當其運算元為假時產生值為true，當運算元為真時產生值為false。 因此，如果陳述P為真，那么¬P（發音為“not P”）將因此為假; 相反，如果¬P為假，則P為真。

¬P的真值表如下：

P	¬P
True	False
False	True

否定可以根據其他邏輯操作來定義。 例如，¬P可以定義為P→⊥（其中→是邏輯結果，⊥是絕對虛假）。 相反，對於任何命題Q（其中∧是邏輯連詞），可以將define定義為Q∧¬Q。 這裡的想法是任何矛盾都是錯誤的。 雖然這些思想既有經典邏輯又有直覺邏輯，但它們並不適用於矛盾的邏輯，而矛盾並不一定是錯誤的。 在經典邏輯中，我們還得到了進一步的同一性，P→Q可以定義為¬P∨Q，其中∨是邏輯析取。

在代數上，經典否定對應於布爾代數中的互補，以及對Heyting代數中的偽實現的直覺否定。 這些代數分別為經典和直覺邏輯提供了語義。

符號

在各種討論環境和套用領域中，對命題P的否定以不同方式表示。 這些變體包括以下內容：

符號	叫法
¬P	Not p
~P	Not p
-P	Not p
Np	En p
	p prime; p complement
	p bar; bar p
!p	Bang p; Not p

在集合論中，∖也用於表示“不是成員”：U∖A是U的所有成員的集合，不是A的成員。無論如何標記或符號化，否定¬P可以被解讀為“不是P”，“不是P”，或者通常更簡單地稱為“非P”。

編程

在數學中，否定被用於計算機科學以構建邏輯陳述。

  if (!(r == t))    {         /*...statements executed when r does NOT equal t...*/    }

“！”表示B，C和具有C語言語言（如C ++，Java，JavaScript，Perl和PHP）的語言中的邏輯NOT。 “NOT”是ALGOL 60，BASIC中使用的運算符，以及具有ALGOL或BASIC啟發語法的語言，如Pascal，Ada，Eiffel和Seed7。某些語言（C ++，Perl等）提供了多個用於否定的運算符。一些語言如PL / I和Ratfor使用¬進行否定。一些現代計算機和作業系統將顯示為！用ASCII編碼的檔案。大多數現代語言允許將上述語句從if(!(r == t))縮短為if（r!= t），這有時允許編譯器/解釋器無法最佳化它，更快的程式。

在計算機科學中，也存在逐位否定。這取得給定的值並將所有二進制1切換為0和0到1。請參閱按位操作。這通常用於在C或C ++中創建一個補碼或“〜”和兩個補碼（簡化為“ - ”或負號，因為它相當於取數字的算術負值），因為它基本上創建了相反的（負值等價物）或數值的數學補充（兩個值加在一起形成一個整體）。

為了獲得給定整數的絕對（正等效）值，以下將起作用，因為“ - ”將其從負變為正（它是負的，因為“x <0”產生真）

 unsigned int abs(int x)    {        if (x < 0)            return -x;        else            return x;    }

為了證明邏輯否定：

 unsigned int abs(int x)    {        if (!(x < 0))            return x;        else            return -x;    }

反轉條件並反轉結果產生邏輯上等同於原始代碼的代碼，即對於任何輸入將具有相同的結果（注意，根據所使用的編譯器，計算機執行的實際指令可能不同）。

這種慣例偶爾會出現在書面語言中，而不是計算機相關的俚語。 例如，投票是指“不投票”。