KAM定理(Kolmogorov-Arnold-Moser theo- rem)研究近可積系統理論的最重要結果之一
內容簡介


可積系統
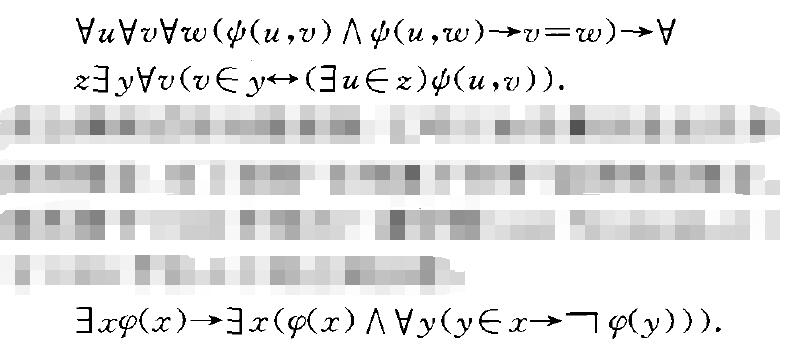
KAM定理(Kolmogorov-Arnold-Moser theo- rem)研究近可積系統理論的最重要結果之一


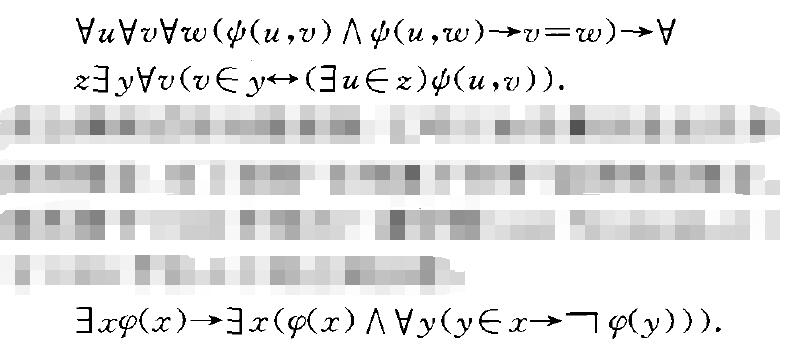
KAM定理(Kolmogorov-Arnold-Moser theo- rem)研究近可積系統理論的最重要結果之一...... KAM定理(Kolmogorov-Arnold-Moser theo- rem)研究近可積系統理論的最重要...
卡姆定理(KAM theorem)也稱為KAM定理,牛頓力學在20世紀的重大進展是。KAM定理是是關於可積哈密頓系統受攝動後其解的長期性態的一個定理。1954年由蘇聯學者A....
《KAM方法和系統的KAM穩定性》從福仲著,由科學出版社於2013年出版...... 的KAM穩定性,包括Kolmogorov型定理、Atropic不變環面、有效穩定性等;第4章給出KAM方法...
3.7 一般均衡理論:阿羅一德布魯存在性定理(1954) 3.8 形式語言理論:喬姆斯基的分類(1957) 3.9 動力系統理論:KAM定理(1962) 3.10 紐結理論:瓊斯的不變數(1984...
《自然定律》是劉德華演唱的一首歌曲,是由黃偉文作詞,Peter Kam作曲和編曲的。該歌曲收錄在專輯《你是我的驕傲演唱會》。...
從50年代到60年代,柯爾莫哥洛夫,Β.И.阿諾爾德和J.K.莫澤對這一情形進行了深入的研究.他們得到的KAM定理(見哈密頓系統)指出:上述狀況經過小擾動並不會消失,...
—— Hamilton系統辛幾何算法KAM定理及其相關方面的研究 尚在久 博士 —— 無窮維Hamilton系統的半離散理論與計算 王雙虎 博士 —— 緊緻Riemann流形上的Hamilton系統...
KAM定理說明接近可積哈密頓系統的運動所具有的性質。由此開始的對哈密頓系統的研究發現,當KAM定理不適用時,系統中也出現混沌運動。在70年代,動力學系統的內在隨機性...
9.6 KAM定理190第3部分 混沌第10章 離散動力系統19410.1 邏輯斯諦方程19410.2 不動點和周期點19610.3 線性差分方程19910.4 不動點附近的局部性態200第...
前言第1章 KAM理論與Arnold擴散1.1 緒論1.1.1 辛流形和Hamilton系統1.1.2 完全可積與近可積系統1.1.3 攝動方法——平均法1.2 KAM定理...
