H方程是一類積分方程,這一類型方程在輻射遷移和中子遷移理論中起到重要作用。
基本介紹
- 中文名:H方程
- 外文名:H-equations
- 適用範圍:數理科學
簡介,發展,積分方程,
簡介
H方程是一類積分方程,這一類型方程在輻射遷移和中子遷移理論中起到重要作用。
下面的方程 稱為H方程,其中ψ(t)是一已知函式,假定它在[0,1]上是非負有界可測的,而H(t)是待求的函式。
稱為H方程,其中ψ(t)是一已知函式,假定它在[0,1]上是非負有界可測的,而H(t)是待求的函式。

發展
H方程的研究開始於20世紀40年代。
1947年,桑德拉塞卡爾(Chandrasekher,S.)、克魯(Crum,M.M.)利用複變函數論的方法,在複平面內考察了方程 ,並給出該方程在半平面Rez>0內解析且在[0,1]上有界的解的存在性條件。克魯木還證明當
,並給出該方程在半平面Rez>0內解析且在[0,1]上有界的解的存在性條件。克魯木還證明當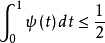 時,則方程僅有一個這樣的解。
時,則方程僅有一個這樣的解。

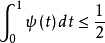
1957年,布斯布里基(Buisbridge,I.W.)在假設ψ(t)為全純函式的條件下,簡化了克魯木結果中的某些討論。
關於H方程的研究現已有了許多重要進展,並把它推廣到某些更一般的形式。
積分方程
積分方程是近代數學的一個重要分支。數學、自然科學和工程技術領域中的許多問題都可以歸結為積分方程問題。正是因為這種雙向聯繫和深入的特點,積分方程論得到了迅速地發展,成為包括眾多研究方向的數學分支。
