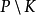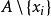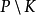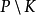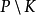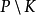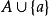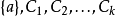基本介紹
- 中文名:Dilworth定理
- 外文名:Dilworth's theorem
- 提出者:Robert P. Dilworth
- 提出時間:1950年
- 套用學科:數學
- 適用領域範圍:離散數學,序理論
定理內容,歸納性證明,
定理內容
反鏈是一種偏序集,其任意兩個元素不可比;而鏈則是一種任意兩個元素可比的偏序集。Dilworth定理說明,存在一個反鏈A與一個將序列劃分為鏈族P的劃分,使得劃分中鏈的數量等於集合A的基數。當存在這種情況時,對任何至多能包含來自P中每一個成員一個元素的反鏈,A一定是此序列中的最大反鏈。同樣地,對於任何最少包含A中的每一個元素的一個鏈的劃分,P也一定是序列可以劃分出的最小鏈族。偏序集的寬度被定義為A與P的共同大小。
另一種Dilworth定理的等價表述是:在有窮偏序集中,任何反鏈最大元素數目等於任何將集合到鏈的劃分中鏈的最小數目。一個關於無限偏序集的理論指出,在此種情況下,一個偏序集具有有限的寬度w,若且唯若它可以劃分為最少w條鏈。
歸納性證明
令P為一有限偏序集,理論認為P為空集時顯然成立。假設P最少有一個元素,令a為P中的極大值。
根據歸納法,假設存在一整數k,使得偏序集 可以被k個不相交的鏈
可以被k個不相交的鏈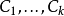 覆蓋,且最少存在一個大小為k的反鏈
覆蓋,且最少存在一個大小為k的反鏈 。顯然,
。顯然, ,
,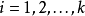 。令
。令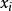 為
為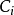 的極大值,
的極大值,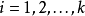 ,
,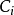 為
為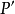 中大小為k的反鏈,令
中大小為k的反鏈,令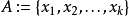 ,
,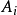 為包含
為包含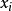 的大小為k的反鏈。確定任意不等的索引
的大小為k的反鏈。確定任意不等的索引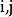 ,那么
,那么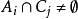 。令
。令 ,根據
,根據 的定義,
的定義, 。因此,由
。因此,由 推斷出
推斷出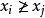 。通過交換
。通過交換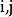 ,可以得到
,可以得到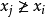 。由此得證,A為反鏈。
。由此得證,A為反鏈。

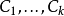


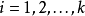
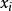
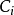
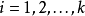
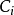
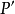
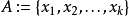
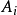
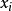
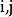
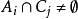




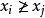
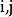
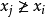
現在來討論P。首先假設, ,
, 。令K為鏈
。令K為鏈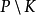 。那么,通過選擇
。那么,通過選擇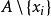 ,使得
,使得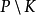 不包含大小為k的反鏈。由於
不包含大小為k的反鏈。由於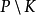 是
是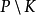 中大小為k-1的反鏈,歸納推出
中大小為k-1的反鏈,歸納推出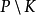 可以被k-1個不相交的鏈覆蓋。因此,正如所需要證明的,P可以被k個不相交的鏈覆蓋。其次,如果
可以被k-1個不相交的鏈覆蓋。因此,正如所需要證明的,P可以被k個不相交的鏈覆蓋。其次,如果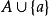 ,
,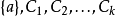 ,那么由於a是P的極大值, 為P中大小為k+1的反鏈。現在,P可以被k+1個鏈 覆蓋。到此,定理全部證明結束。
,那么由於a是P的極大值, 為P中大小為k+1的反鏈。現在,P可以被k+1個鏈 覆蓋。到此,定理全部證明結束。