基本介紹
- 中文名：狄爾沃斯定理
- 外文名：Dilworth's theorem
- 別稱：Dilworth定理
- 所屬學科：數學（組合設計）
- 簡介：關於偏序集的極大極小的定理
基本介紹,相關介紹,
基本介紹
定理 對偏序集<A，≤>，設A中最長鏈的長度是n，則將A中元素分成不相交的反鏈，反鏈個數至少是n。
證明施歸納於n。
當n=1時，A本身就是一條反鏈，定理結論成立。(這時≤是恆等關係)。
假設對於n=k，結論成立。考慮n=k+1的情況，當A中最長鏈的長度為k+1時，令M為A中極大元的集合，顯然M是一條反鏈。而且A-M中最長鏈的長度為k。由歸納假設，可以把A-M分成至少k個不相交的反鏈，加上反鏈M，則A可分成至少k+1條反鏈。
這個定理稱為狄爾沃斯(Dilworth)定理或偏序集的分解定理，這是組合學三大存在性定理之一，有廣泛的套用。這種分解是所有分解方法中反鏈個數最少的一種分解方法，因為A不可能分解成n-1條反鏈。假若只有n-1條反鏈，那么最長鏈的n個元素中必有2個元素被分到同一個反鏈，顯然這與反鏈的定義矛盾。
有窮偏序集分解成n條反鏈的過程可以採用下面的方法去做。
算法 偏序集反鏈分解算法：
輸入：偏序集A．
輸出：A中的反鏈
．
1．i←1
2．
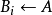的所有極大元的集合(顯然
是一條反鏈)
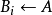
3．令
．
4．if A≠∅
5．
6．轉2
注意：從A中去掉Bi中的元素時，同時去掉連線這些元素與被它覆蓋的元素之間的邊，行2~3每執行一次，最長鏈的長度減少l，同時產生一條新的反鏈。因為最長鏈長度為n，恰好執行n次，算法結束，並得到n條反鏈。
推論 對偏序集<A，≤>，若A中元素為mn+1個，則A中或者存在一條長度為m+1的反鏈，或者存在一條長度為n+1的鏈。
相關介紹
組合數學中有很多存在性定理，其中三大基本定理是經常使用的工具：一是1935年P.Hall提出的“相異代表組定理”；二是1950年R.P.Dilworth發現的“偏序集分解定理（狄爾沃斯定理）”；三是1930年F.P.Ramsey發表的“廣義鴿洞原理”。
關於R.P.Dilworth的狄爾沃斯定理的相關介紹：
大家知道，許多離散事物對象之間存在著種種“次序”關係，例如一組事物的排隊，某些現象出現的先後，生物的代代相傳等，但也不是任何一類事物間都有同一種“序”的關係，因此近代數學從無數具體的對象關係里抽象出來的“偏序集”(即半序集)概念，就顯得更加重要而有用，現代組合數學中的若干重要理論就是建立在偏序集概念的基礎上的。
由有限個元素(離散事物)所構成的有限偏序集往往可分解成若干條“鏈”(即有起始元的全序子集)，位於不同鏈上的元素之間可以沒有序關係，這些沒有序關係的元素叫作“無序元”，由無序元所作成的子集叫作無序子集，那么，把一個偏序集分解成鏈的最少條數m和該偏序集所含最大無序子集的元素個數M之間有什麼關係呢?Dilworth發現它們之間恰好具有相等關係：m=M。這個定理也是利用精細的歸納法證明的，它不僅對一般組合數學十分重要，而且對生物科學也有很大用處。例如，由這個定理可以推斷：在mn+1個實驗用的小鼠中，要么有m+1個是代代相傳的，要么有n+1個是彼此沒有親緣關係的。”(這裡可把上下代關係看作序的關係，故mn+1個小鼠作成一個偏序集)。
