Debye模型

Debye模型是由Peter Debye在1912年開發的一種方法，用於估算聲子對固體中比熱（熱容量）的貢獻。 它將原子晶格（熱）的振動視為一個盒子中的聲子，與愛因斯坦模型相比，愛因斯坦模型將固體視為許多獨立的非相互作用的量子諧振子。 德拜模型正確地預測了熱容量的低溫依賴性，其與T比值成正比。這是德拜T3定律。 就像愛因斯坦模型一樣，它也在高溫下恢復了杜隆 - 珀蒂定律。 但由於簡化的假設，其準確度在中等溫度下受損。

基本介紹

• 中文名：Debye模型
• 外文名：Debye model

Debye的推導

事實上，Debye的推導方式有點不同，也更簡單。 利用連續介質力學，他發現頻率小於特定值的振動態的數量是漸近的：

其中 是體積， 是由彈性係數和密度計算的因子。 結合這個公式和諧振子在溫度 下的期望能量（愛因斯坦在他的模型中已經使用過）會給出一個能量：

如果振動頻率持續到無窮大. 這種形式給出了在低溫下正確的 行為. 但德拜意識到 原子的振動態不能超過 他做了一個假設，即在原子固體中，振動態的頻率譜將繼續遵循上述規則，最高頻率 被選擇為使得狀態的總數為 ：

Debye知道這個假設並不是真的正確（高頻率的間隔比假定的要高），但它確保了高溫下的適當行為。 能量然後由下式給出：

,

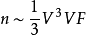
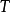
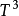
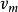
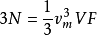
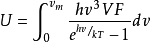
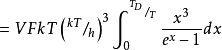
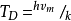
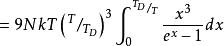
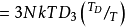
其中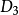 是稍後給出三階Debye函式名稱的函式。

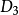
Debye的溫度表

即使Debye模型不完全正確，它也可以很好地近似於其他貢獻（例如高度移動的傳導電子）可忽略不計的絕緣結晶固體的低溫熱容量。 對於金屬來說，電子對熱量的貢獻與T成正比，T在低溫下主導Debye T3晶格振動的結果。 在這種情況下，德拜模型只能說近似於晶格對比熱的貢獻。下表列出了幾種純元素的Debye溫度：

鋁	428 K	錳	410 K
鈹	1440 K	鎳	450K
鎘	209 K	白金	240K
銫	38 K	藍寶石	1047 K
碳	2230 K	矽	645 K
鉻	630 K	銀	215 K
銅	343.5 K	鉭	240 K
黃金	170 K	錫（白）	（白）200 K
鐵	470 K	鈦	420 K
鉛	105 K	鎢	400 K

Debye模型與實驗數據的擬合通常通過允許Debye溫度與溫度相關而在現象上得到改善，例如，隨著溫度的升高，水凍的值從約222K增加到300K 從絕對零度到大約100 K。