基本介紹
- 中文名:C4.5算法
概述
改進表現
優缺點
算法描述
屬性選擇度量






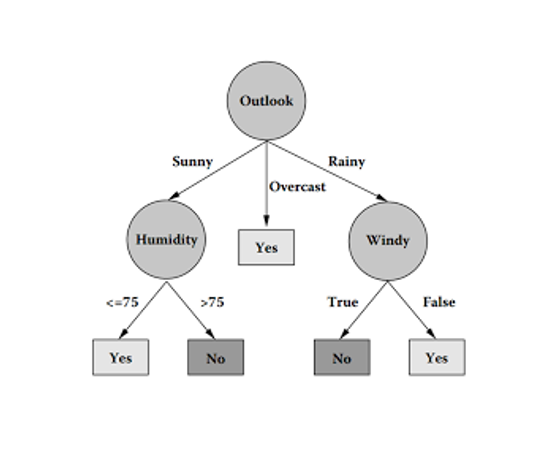






C4.5算法是由Ross Quinlan開發的用於產生決策樹的算法。該算法是對Ross Quinlan之前開發的ID3算法的一個擴展。C4.5算法產生的決策樹可以被用作分類目的,因此該算法也...
C4.5 算法是機器學習算法中的一種分類決策樹算法,其核心算法是 ID3 算法。...... C4.5 算法是機器學習算法中的一種分類決策樹算法,其核心算法是 ID3 算法。...
國際權威的學術組織,數據挖掘國際會議ICDM (the IEEE International Conference on Data Mining)在2006年12月評選出了數據挖掘領域的十大經典算法中,C4.5算法排名第一...
6.5 c4.5算法:生成決策規則6.6 cart算法和gini指標6.7 決策樹和決策規則的局限性6.8 複習題6.9 參考書目第7章 人工神經網路7.1 人工神經元的模型...
C4.5就是一個決策樹算法,它是決策樹(決策樹也就是做決策的節點間像一棵樹一樣的組織方式,其實是一個倒樹)核心算法ID3的改進算法,所以基本上了解了一半決策樹...
作為一本教科書,本書全面講述了數據挖掘的概念、模型、方法和算法。本書共包括...7.2C4.5算法:生成一個決策樹 1227.3未知屬性值 1287.4修剪決策樹 132...
這是一本基於公理研究學習算法的書。共 17章,由兩部分組成。第一部分是機器...14.3增益比率與C4.5算法...19414.4Gini指數與CART算法......
3.2.7 算法評估 3.3 C4.5算法 3.3.1 信息增益率 3.3.2 C4.5的實現 3.3.3 訓練決策樹 3.3.4 分類數據 3.4 Scikit-Learn與回歸樹 3.4.1 回歸算...
C4.5是ID3的一個改進算法。...... 由於ID3算法在實際套用中存在一些問題,於是Quinlan提出了C4.5算法C4.5算法 編輯 C4.5算法繼承了ID3算法的優點,並在以下幾方面對ID3...
6.5C4.5算法:生成決策規則 1436.6CART算法和Gini指標 1466.7決策樹和決策規則的局限性 148 [2] 6.8複習題 1506.9參考書目 153...
C4.5算法繼承了ID3算法的優點,並在以下幾方面對ID3算法進行了改進:1) 用信息增益率來選擇屬性,克服了用信息增益選擇屬性時偏向選擇取值多的屬性的不足;2) 在樹...
還有其他很多決策樹算法,常見的有:ID3算法 C4.5算法 CHi-squared Automatic Interaction Detector (CHAID), 在生成樹的過程中用多層分裂 [2] 。 MARS可以更好...
5.3.11d3算法5.3.2 c4.5的生成算法5.4決策樹的剪枝5.5cart算法5.5.1cart生成5.5.2cart剪枝本章概要繼續閱讀習題參考文獻第6章邏輯斯諦回歸與最大熵模型...
10.3ID3算法實例分析10.4ID3算法的特點及套用10.4.1ID3算法的特點10.4.2ID3算法的套用10.5ID3算法源程式結果分析10.6決策樹分類算法——C4.5算法原理...
2.4.1 C4.5算法2.4.2 隨機決策樹算法2.4.3 隨機森林算法參考文獻3 人工神經網路和遺傳算法3.1 人工神經網路3.1.1 反向人工神經網路...
5.3 ID3算法5.4 C4.5算法5.5 CART算法5.6 Clementine輔助決策樹建立5.7 決策樹的評價標準5.8 決策樹的剪枝5.9 決策樹的最佳化5.10 燃氣管網安全預測案例分析與...
第3章 分類算法 3.1 分類算法概述 3.1.1 分類模型訓練階段 3.1.2 分類模型評估階段 3.1.3 分類階段 3.2 分類算法的套用 3.3 C4.5分類算法 3.3...
