Binet-Cauchy定理,即比內-柯西定理描述了矩陣的乘積與行列式的關係·
基本介紹
- 中文名:Binet-Cauchy定理
- 概述:Binet-Cauchy定理
- 定理的內容:設A,B分別為矩陣,
- 定理的證明:我們令A=(aij),B=(bij),AB=
定理的內容,定理的證明,
定理的內容
設A,B分別為 矩陣,則有det(AB)=
矩陣,則有det(AB)=

(1) 0,當n>s
(2)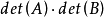 ,當n=s
,當n=s
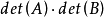
(3)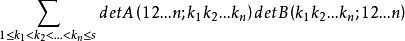 ,當n
,當n s
s
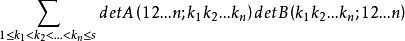
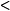
其中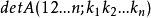 表示A的第
表示A的第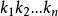 列所成的子式,而其中
列所成的子式,而其中 表示B的第
表示B的第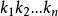 行所成的子式。
行所成的子式。
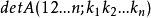
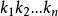

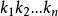
定理的證明
我們令A=(aij),B=(bij),AB=C=(cij).可以構造n+s階方陣M,分塊為
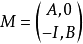
其中I為單位方陣. 下面用兩種方法計算M的行列式.
把M的第n+1,n+2......n+s行的第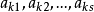 倍加到第k行去.(k=1,2......n)
倍加到第k行去.(k=1,2......n)
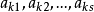
如此,M的第k行就化為了:
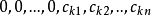
方陣M化為了方陣N
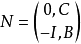
顯然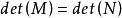 。再利用Laplace展開定理,對N的前n行進行展開,就有
。再利用Laplace展開定理,對N的前n行進行展開,就有
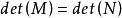
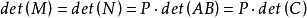
其中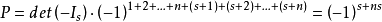
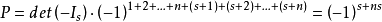
對M的前n行直接做Laplace展開定理:
(1)當n>s時,M的前n行子式都為0,detM=0,則detC=det(AB)=0.
(2)當n=s時,只有A這個子式非0,det(AB)=det(A)*det(B).
(3)當n<s時,計算所有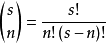 個非零子式(
個非零子式(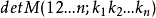 )與其代數餘子式為:
)與其代數餘子式為:
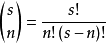
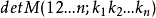

這裡,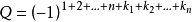 ,而
,而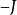 為
為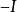 中刪去第
中刪去第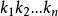 列所得的矩陣,即-J的第
列所得的矩陣,即-J的第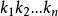 行全為0。
行全為0。
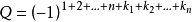
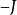
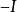
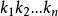
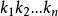
用Laplace展開定理,按第k1,k2...kn行展開,注意到這n行在-I'的部分是0,所以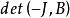 只有一個可能非零的子式,那就是B的第k1,......kn行所構成的子式
只有一個可能非零的子式,那就是B的第k1,......kn行所構成的子式 。也就是說,
。也就是說,
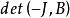

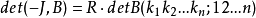
這裡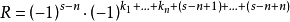
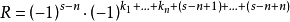
最後,我們總結上述結論並結合(一)的結論,就有
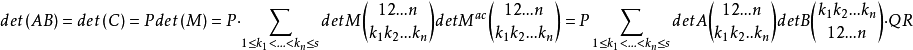
而PQR=1,定理得證
