基本介紹
- 中文名:B-S模型
- 全稱:期權定價模型
- 名字來源:BLACK、SCHOLES名字的縮寫
- 目的:紀念他們發現該模型
成立條件
計算方法

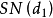





BS模型一般指本詞條

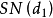




簡稱BS模型.適用於歐式權證 ...... 簡稱BS模型.適用於歐式權證詞條標籤: 社會事件 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者...
B-S是兩位經濟學家BLACK、SCHOLES名字的縮寫,為了紀念他們發現該模型而用他們的名字命名。 在二叉樹的期權定價模型中,如果標的證券期末價格的可能性無限增多時,其...
布萊克-舒爾斯模型(英語:Black-Scholes Model),簡稱BS模型,是一種為期權或權證等金融衍生工具定價的數學模型,由美國經濟學家邁倫·舒爾斯(Myron Scholes)與費雪·...
BS.Play是一套開放原始碼,可以提供libcomoroclient 同樣的功能。...... BS.Play是一套開放原始碼,可以提供libcomoro...採用單進程靜態多執行緒的事件 驅動模型,可以...
布萊克-舒爾斯模型(英語:Black-Scholes Model),簡稱BS模型,又稱布萊克-舒爾斯-墨頓模型(Black–Scholes–Merton model),是一種為期權或權證等金融衍生工具定價的...
個人BS法又叫個人頭腦風暴法、個人智力激勵法。BS是英文Brain Storming的縮寫。這是一種將頭腦風暴法套用於個人領域,提高個人創造性的方法。...
例如氟鈹化鋰Li2BeF4可作為正矽酸鋅Zn2SiO4的模型物質。又如其他相對應的模型物質對BeF2-SiO2,LiF-MgO,MgF2-TiO2,CaF2-ThO2,KMgF3-SrTiO3,RbBF4-BsSO4和...
《運籌學方法與模型》是由復旦大學出版社出版的一部教育作品,作者是傅家良。...... 《運籌學方法與模型》是由復旦大學出版...2.5.2 參數bs的靈敏度分析 2.5.3 ...
(高達模型的一種系列)編輯 鎖定 討論999 萬代公司2010推出的新系列RG(REAL ...RX-0 獨角獸高達2號機 報喪女妖 VN/BS裝甲擴張單元套裝 [2] 首次發售日期:...
6BS品牌創建與管理系統(簡稱6BS)品牌是一門科學,我們只有真正理解品牌的本質和原理,找到創建品牌的關鍵要素和規律,我們的品牌建設才具有意義。...
《運籌學方法與模型(第2版)》是2014年出版的圖書,作者是傅家良。...... 《運籌學方法與模型(第2版)》是2014年出版...2.5.2參數bs的靈敏度分析 2.5.3增加新的...
隱含波動率(Implied Volatility)是將市場上的期權或權證交易價格代入權證理論價格模型<Black-Scholes模型>,反推出來的波動率數值。由於期權定價模型(如BS模型)給出了...
