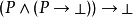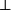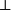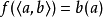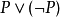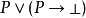BHK釋義

在數理邏輯中，直覺主義邏輯的布勞威爾-海廷-柯爾莫哥洛夫釋義或BHK釋義是由魯伊茲·布勞威爾、阿蘭德·海廷和獨立的由安德雷·柯爾莫哥洛夫提出的。它有時也叫做可實現性釋義，因為有關於史蒂芬·科爾·克萊尼的可實現性理論。

基本介紹

• 中文名：BHK釋義
• 外文名：The BHK interpretation
• 學科：數學證明
• 提出者：魯伊茲·布勞威爾、阿蘭德·海廷
• 別名：可實現性釋義
• 有關術語：可實現性

釋義

釋義精確的陳述一個給定的公式的證明是什麼。這是通過這個公式的在結構上歸納規定的：

的證明是有序對<a,b>，這裡的a是P的一個證明而b是Q的一個證明。

的證明是有序對<a,b>，這裡的a是0而b是P的證明，或者a是1而b是Q的證明。

的證明是函式f: P→Q，它把P的證明變換成Q的證明。

的證明是有序對<a,b>，這裡的a是S的一個元素，而b是φ(a)的一個證明。

的證明是函式f: a→φ(a)，它把S的一個元素a變換成φ(a)的證明。

的證明被定義為 ，它的證明是把P的證明變換成的證明的一個函式。

是荒謬。應當沒有它的證明。

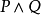
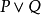
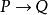
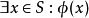
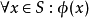
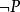
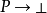
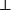
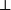
假定從上下文獲知原始命題的釋義。

荒謬與函式

邏輯系統不可能有形式否定運算元，使得在沒有P的證明的時候有正確的 非P的證明（參見哥德爾不完備定理）。BHK釋義轉而採納 非P為意味著P導致荒謬，指示為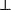，所以¬P的證明是把P的證明變換成荒謬的證明的函式。

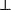
荒謬的標準例子可以在算術中找到。假定0=1，並進行數學歸納法：0=0通過等同公理得到；（歸納假設）如果0等於特定自然數n，則1將等於n+1 (皮亞諾公理：Sm = Sn若且唯若m = n)，但是因為0=1，所以0也等於n+1；通過歸納，0等於任何數，所以任何兩個自然數都是相等的。

所以，有從0=1的證明得到任何基本算數等式和進而任何複雜算術命題的一種方式。進一步的說，要得到這種結果，不是必須的涉及皮亞諾公理0不是任何自然數的後繼。這使得0=1在Heyting算術（皮亞諾公理被重寫0=Sn → 0=S0）適合充當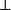 。這種0=1的使用驗證了爆炸原理。

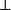
BHK釋義依賴於制定把一個證明變換成另一個證明，或者把一個域的元素變換成一個證明的函式的觀點。不同版本的數學構造主義在這一點上是有分歧的。

Kleene的可實現性理論把這種函式看成是可計算函式。它處理Heyting算術，這裡的量化的域是自然數而原始命題有x=y的形式。x=y的證明簡單是平凡的算法，如果x求值得到與y求值同樣的數（它對於自然數總是可決定的），否則沒有證明。可以通過歸納建造起更複雜的算法。

可實現性

可實現性是可用來處理關於公式的信息而不是關於公式的證明的那部分證明論。自然數n被稱為實現了自然數算術的語言中一個陳述。其他邏輯和數學陳述也是可實現的，假如提供了解釋合式公式一種方法，而不用藉助達成這些公式的證明。

史蒂芬·科爾·克萊尼在1945年介入了可實現性的概念，寄希望於它成為直覺邏輯推理的忠實典範，但這個構想最初由Rose反證了一個可實現的命題公式的例子，它在直覺演算中是不可證明的。可實現性似乎由於它的複雜度而難於公理化，但它可以通過高階Heyting算術（HA）來達成。

改進可實現性使用有類型lambda演算作為語言實現者。改進可實現性是展示馬爾科夫原理在直覺邏輯中不可推導的一種方式。正相反，它允許構造性的證實前提的獨立性原理： 。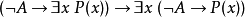

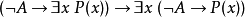
相對可實現性是非必需可計算的數據結構的遞歸或遞歸可枚舉元素的直覺主義分析，比如在實數在數字計算機系統上只能近似表示的時候在所有實數上的可計算的運算。在計算機科學套用：改進可實現性證實了實施於某些證明輔助工具比如Coq中的“證明提取”過程。

直覺類型論與直覺主義邏輯

經典邏輯是理想主義的，純教條的。構造邏輯是現實主義的，它給數學公式經驗的內容。直覺主義邏輯更多地從證明論和模型論的角度展現邏輯：也就是說，它是一個構造的邏輯。所謂構造性是指：與經典邏輯只關心公式的真值不同，構造邏輯關注的是實際的證明對象本身。但是什麼是構造呢?“構造”可以指一個過程以及執行該過程的結果。

直覺類型論、或構造類型論、或Martin-Löf 類型論、或就叫類型論是基於數學構造主義的函式式程式語言、邏輯和集合論。直覺類型論由瑞典數學家和哲學家 Per Martin-Löf 在1972年介入。 Martin-Löf 已經多次修改了它的提議；先是非直謂性的而後是直謂性的，先是外延的而後是內涵的類型論變體。直覺類型論基於的是命題和類型的同一: 一個命題同一於它的證明的類型。這種同一通常叫做Curry-Howard同構，它最初公式化了命題邏輯和簡單類型 lambda 演算。類型論通過介入包含著值的依賴類型把這種同一擴展到謂詞邏輯。類型論內在化了 Brouwer、Heyting 和 Kolmogorov 提議的叫做 BHK釋義的直覺邏輯釋義。類型論的類型扮演了類似於集合在集合論的角色，但是在類型論中的函式總是可計算的。

直覺主義邏輯或構造性邏輯是最初由阿蘭德·海廷開發的為魯伊茲·布勞威爾的數學直覺主義計畫提供形式基礎的符號邏輯。這個系統保持跨越生成導出命題的變換的證實性而不是真理性。從實用的觀點，也有使用直覺邏輯的強烈動機，因為它有存在性質，這使它還適合其他形式的數學構造主義。直覺邏輯的公式的語法類似於命題邏輯或一階邏輯。但是直覺邏輯的連結詞不像經典邏輯那樣是可互定義的，因此它們的選擇是重要的。在直覺命題邏輯中通常使用 →, ∧, ∨, ⊥ 作為基本連結詞，把 ¬ 作為 ¬A = (A → ⊥) 的簡寫處理。在直覺一階邏輯中量詞 ∃, ∀ 都是需要的。不同在於很多經典邏輯的重言式在直覺邏輯中不再是可證明的。例子不只包括排中律 P ∨ ¬P，還有皮爾士定律 ((P → Q) → P) → P，甚至還有雙重否定除去。在經典邏輯中，P → ¬¬P 和 ¬¬P → P 二者都是定理。在直覺邏輯中，只有前者是定理: 雙重否定可以介入但不能除去。對很多經典有效重言式不是直覺邏輯的定理的觀察導致了弱化經典邏輯的證明論的想法。

示例

恆等函式是公式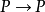的證明，不管P是什麼。

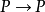
無矛盾律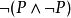被展開為：

的證明是函式f，它把 的證明變換成 的證明。

的證明是證明的有序對<a,b>，這裡的a是P的證明，而b是的證明。

的證明是把P的證明變換成的證明的函式。

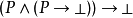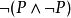
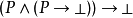
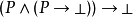
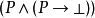
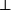
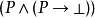
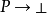
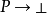
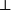
把它們放置到一起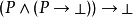，的證明是函式f，它把有序對<a,b>變換成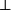的證明 -- 這裡的a是P的證明，而b是把P的證明變換成 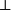的證明的一個函式。函式 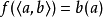證明了無矛盾律，不管P是什麼。在另一方面，排中律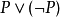展開為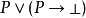，而一般沒有證明。