AVL在計算機科學中是最先發明的自平衡二叉查找樹。
基本介紹
- 中文名：AVL樹
- 外文名：AVL（Adelson-Velskii and Landis）
- 發明者： G.M. Adelson-Velsky
- 年份：1962 年
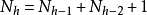
簡介,計算,操作,插入,刪除,查找,
簡介
AVL（Adelson-Velskii and Landis）樹得名於它的發明者 G.M. Adelson-Velsky 和 E.M. Landis，他們在 1962 年的論文《An algorithm for the organization of information》中發表了它 。
計算
高度為 h 的 AVL 樹，節點數 N 最多
； 最少 （其中）。
最少節點數 n 如以斐波那契數列可以用數學歸納法證明：
即：
換句話說，當節點數為 N 時，高度 h 最多為
.
節點的平衡因子是它的左子樹的高度減去它的右子樹的高度。帶有平衡因子 1、0 或 -1 的節點被認為是平衡的。帶有平衡因子 -2 或 2 的節點被認為是不平衡的，並需要重新平衡這個樹。平衡因子可以直接存儲在每個節點中，或從可能存儲在節點中的子樹高度計算出來。
操作
AVL樹的基本操作一般涉及運做同在不平衡的二叉查找樹所運做的同樣的算法。但是要進行預先或隨後做一次或多次所謂的"AVL 旋轉"。
AVL 旋轉操作分為左旋轉 (left rotation) 和右旋轉 (right rotation)，可以用下圖表示。其中T1, T2和T3都是帶旋轉樹的子樹。
y x / \ 右旋轉 (y) / \ x T3 – – – – – – – > T1 y / \ < - - - - - - - / \ T1 T2 左旋轉 (x) T2 T3
AVL 旋轉操作並不會改變二叉查找樹 (BST) 應滿足的性質，也就是說，keys(T1) < key(x) < keys(T2) < key(y) < keys(T3) 依然成立。
假設由於在二叉排序樹上插入結點而失去平衡的最小子樹根結點為z（即z是離插入點最近，且平衡因子絕對值超過1的祖先結點），則失去平衡後進行進行的規律可歸納為下列四種情況：
單向右旋平衡處理 (Left Left)：由於在z的左子樹根結點y的左子樹（根節點為x）上插入結點，z的平衡因子由1增至2，致使以z為根的子樹失去平衡，則需進行一次右旋轉操作，具體操作如下所示；
z y / \ / \ y T4 右旋轉 (z) x z / \ - - - - - - - - -> / \ / \ x T3 T1 T2 T3 T4 / \ T1 T2
單向左旋平衡處理 (Right Right)：由於在z的右子樹根結點y的右子樹（根節點為x）上插入結點，z的平衡因子由-1變為-2，致使以z為根的子樹失去平衡，則需進行一次左旋轉操作，具體操作如下所示；
z y / \ / \ T1 y 左旋轉 (z) z x / \ - - - - - - - -> / \ / \ T2 x T1 T2 T3 T4 / \ T3 T4
雙向旋轉（先左後右）平衡處理 (Left Right)：由於在z的左子樹根結點y的右子樹（根節點為x）上插入結點，z的平衡因子由1增至2，致使以z為根的子樹失去平衡，則需進行兩次旋轉（先左旋後右旋）操作，具體操作如下所示。
z z x / \ / \ / \ y T4 左旋轉 (y) x T4 右旋轉 (z) y z / \ - - - - - - - - -> / \ - - - - - - - -> / \ / \T1 x y T3 T1 T2 T3 T4 / \ / \ T2 T3 T1 T2
雙向旋轉（先右後左）平衡處理 (Right Left)：由於在z的右子樹根結點y的左子樹（根節點為x）上插入結點，z的平衡因子由-1變為-2，致使以z為根的子樹失去平衡，則需進行兩次旋轉（先右旋後左旋）操作，具體操作如下所示。
z z x / \ / \ / \ T1 y 右旋轉 (y) T1 x 左旋轉 (z) z y / \ - - - - - - - - -> / \ - - - - - - - -> / \ / \ x T4 T2 y T1 T2 T3 T4 / \ / \T2 T3 T3 T4
插入
向AVL樹插入可以通過如同它是未平衡的二叉查找樹一樣把給定的值插入樹中，接著自底向上向根節點折回，於在插入期間成為不平衡的所有節點上進行旋轉來完成。因為折回到根節點的路途上最多有 1.5 乘 log n 個節點，而每次 AVL 旋轉都耗費恆定的時間，插入處理在整體上耗費 O(log n) 時間。 在平衡的二叉排序樹Balanced BST (BBST) 上插入一個新的數據元素e的遞歸算法可描述如下： 若BBST為空樹，則插入一個數據元素為e的新結點作為BBST的根結點，樹的深度增1； 若e的關鍵字和BBST的根結點的關鍵字相等，則不進行； 若e的關鍵字小於BBST的根結點的關鍵字，而且在BBST的左子樹中不存在和e有相同關鍵字的結點，則將e插入在BBST的左子樹上，並且當插入之後的左子樹深度增加（+1）時，分別就下列不同情況處理之： BBST的根結點的平衡因子為-1（右子樹的深度大於左子樹的深度，則將根結點的平衡因子更改為0，BBST的深度不變； BBST的根結點的平衡因子為0（左、右子樹的深度相等）：則將根結點的平衡因子更改為1，BBST的深度增1； BBST的根結點的平衡因子為1（左子樹的深度大於右子樹的深度）：則若BBST的左子樹根結點的平衡因子為1：則需進行單向右旋平衡處理，並且在右旋處理之後，將根結點和其右子樹根結點的平衡因子更改為0，樹的深度不變； 若e的關鍵字大於BBST的根結點的關鍵字，而且在BBST的右子樹中不存在和e有相同關鍵字的結點，則將e插入在BBST的右子樹上，並且當插入之後的右子樹深度增加（+1）時，分別就不同情況處理之。插入操作的示例代碼如下 ，
// Recursive function to insert a key in the subtree rooted// with node and returns the new root of the subtree.struct Node* insert(struct Node* node, int key){ /* 1. Perform the normal BST insertion */ if (node == NULL) return(newNode(key)); if (key < node->key) node->left = insert(node->left, key); else if (key > node->key) node->right = insert(node->right, key); else // Equal keys are not allowed in BST return node; /* 2. Update height of this ancestor node */ node->height = 1 + max(height(node->left), height(node->right)); /* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */ int balance = getBalance(node); // If this node becomes unbalanced, then // there are 4 cases // Left Left Case if (balance > 1 && key < node->left->key) return rightRotate(node); // Right Right Case if (balance < -1 && key > node->right->key) return leftRotate(node); // Left Right Case if (balance > 1 && key > node->left->key) { node->left = leftRotate(node->left); return rightRotate(node); } // Right Left Case if (balance < -1 && key < node->right->key) { node->right = rightRotate(node->right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node;} 實際上，旋轉操作最多被執行一次。當我們插入了節點，並找到了第一個不平衡節點z，對節點z進行平衡操作後，以z為根的子樹的高度就和未插入節點前的高度一樣了，所以我們只需要進行一次旋轉操作即可 。
刪除
從AVL樹中刪除可以通過如同它是未平衡的二叉查找樹一樣把給定的值刪除，接著從刪除值以前所在節點位置向上找到第一個不平衡節點。讓z為該不平衡節點，y是z的最高的子節點，x是y最高的子節點，我們可以如插入操作時，根據z, y 和 x的排布情況來旋轉子樹使該子樹平衡。值得注意的是，使得第一個不平衡節點為根的子樹平衡後，我們還需要繼續向上尋找不平衡節點，直至整個樹平衡為止。因為樹的高度為 log(n), 旋轉的時間複雜度為 O(1), 故刪除的時間複雜度仍為O(log(n))。刪除操作的示例代碼如下 ，
// Recursive function to delete a node with given key// from subtree with given root. It returns root of// the modified subtree.struct Node* deleteNode(struct Node* root, int key){ // STEP 1: PERFORM STANDARD BST DELETE if (root == NULL) return root; // If the key to be deleted is smaller than the // root's key, then it lies in left subtree if ( key < root->key ) root->left = deleteNode(root->left, key); // If the key to be deleted is greater than the // root's key, then it lies in right subtree else if( key > root->key ) root->right = deleteNode(root->right, key); // if key is same as root's key, then This is // the node to be deleted else { // node with only one child or no child if( (root->left == NULL) || (root->right == NULL) ) { struct Node *temp = root->left ? root->left : root->right; // No child case if (temp == NULL) { temp = root; root = NULL; } else // One child case *root = *temp; // Copy the contents of // the non-empty child free(temp); } else { // node with two children: Get the inorder // successor (smallest in the right subtree) struct Node* temp = minValueNode(root->right); // Copy the inorder successor's data to this node root->key = temp->key; // Delete the inorder successor root->right = deleteNode(root->right, temp->key); } } // If the tree had only one node then return if (root == NULL) return root; // STEP 2: UPDATE HEIGHT OF THE CURRENT NODE root->height = 1 + max(height(root->left), height(root->right)); // STEP 3: GET THE BALANCE FACTOR OF THIS NODE (to // check whether this node became unbalanced) int balance = getBalance(root); // If this node becomes unbalanced, then there are 4 cases // Left Left Case if (balance > 1 && getBalance(root->left) >= 0) return rightRotate(root); // Left Right Case if (balance > 1 && getBalance(root->left) < 0) { root->left = leftRotate(root->left); return rightRotate(root); } // Right Right Case if (balance < -1 && getBalance(root->right) <= 0) return leftRotate(root); // Right Left Case if (balance < -1 && getBalance(root->right) > 0) { root->right = rightRotate(root->right); return leftRotate(root); } return root;} 查找
在AVL樹中查找同在一般BST完全一樣的進行，所以耗費 O(log n) 時間，因為AVL樹總是保持平衡的。不需要特殊的準備，樹的結構不會由於查詢而改變。（這是與伸展樹查找相對立的，它會因為查找而變更樹結構。）
