天文單位(天文單位)

天文單位是天文學中計量天體之間距離的一種單位。以A.U.表示，其數值取地球和太陽之間的平均距離。國際天文學聯合會1964年決定採用1A.U.=1.496x10^8千米，自1968年使用至1983年底；又於1978年決定改用1A.U.=149597870千米，從1984年開始使用。此常數在20世紀60年代以前系由所測的太陽視差計算得出；60年代以後則據雷達天文觀測，由光速和單位距離光行差tA 導出。一般用以計量太陽系中各天體間的距離。

基本介紹

• 中文名：天文單位
• 外文名：Astronomical Unit
• 換算：149597870700米
• 含義：長度單位
• 符號：AU

歷史沿革

“天文單位”一詞出現於1903年。1938年以前，天文單位是指在沒有大行星攝動作用（見攝動理論）下，從地月系質心到太陽的平均距離，或者說地月系質心繞太陽公轉的無攝動橢圓軌道的半長徑。

1976年國際天文學聯合會頒布了一系列天文研究採用的最重要單位，其中之一就是被稱為“天文單位”（簡寫為AU）的日地距離。按照國際天文學聯合會的原始定義，日地距離是“在太陽引力作用下沿以太陽中心為圓心的圓軌道，以每天0.01720209895弧度的角速度運動的無質量粒子的軌道半徑”。當時公布的數據為1天文單位等於149597870.691千米。

這樣定義的日地距離除了定義本身晦澀難懂外，還有個讓人很難接受的問題：既然是“基本單位”，似乎應該是個定數，但按照1976年國際天文學聯合會的定義，天文單位是個不斷變化的數值。首先，太陽的質量在不斷減小，導致天文單位的數值也在緩慢改變。其次，根據廣義相對論，時空的定義是相對的，與觀測者所處的時空有關。按照上述定義，在太陽系內不同地方測量到的天文單位數值就會不同，比方說在木星（太陽系內質量最大的行星）上測得的天文單位與在地球上測得的要相差1000多千米。

天文單位

正是為了解決這樣的問題，2012年8月30日第28屆國際天文學聯合會大會發表了B2決議，全票通過更改天文單位的定義。規定將天文單位的長度確定為149597870700米，不再是一個不斷變化的數值。

計算方法

天文學家利用三角視差法、分光視差法、星團視差法、統計視差法、造父視差法和力學視差法等，測定恆星與我們的距離。恆星距離的測定，對研究恆星的空間位置、求得恆星的光度和運動速度等，均有重要的意義。

天文單位

離太陽距離在16光年以內的有50多顆恆星。其中最近的是半人馬座比鄰星，距太陽約4．2光年，大約是40萬億千米。

三角視差法

測量天體之間的距離可不是一件容易的事。 天文學家把需要測量的天體按遠近不同分成好幾個等級。離我們比較近的天體，它們離我們最遠不超過100光年（1光年=9.46×10¹²千米），天文學家用三角視差法測量它們的距離。三角視差法是把被測的那個天體置於一個特大三角形的頂點，地球繞太陽公轉的軌道直徑的兩端是這個三角形的另外二個頂點，通過測量地球到那個天體的視角，再用到已知的地球繞太陽公轉軌道的直徑，依靠三角公式就能推算出那個天體到我們的距離了。稍遠一點的天體我們無法用三角視差法測量它和地球之間的距離，因為在地球上再也不能精確地測定他它們的視差了。

移動星團法

這時我們要用運動學的方法來測量距離，運動學的方法在天文學中也叫移動星團法，根據它們的運動速度來確定距離。不過在用運動學方法時還必須假定移動星團中所有的恆星是以相等和平行的速度在銀河系中移動的。在銀河系之外的天體，運動學的方法也不能測定它們與地球之間的距離。

造父視差法

造父視差法又叫標準燭光法。

物理學中有一個關於光度、亮度和距離關係的公式。S∝L0/r2

測量出天體的光度L0和亮度S，然後利用這個公式就知道天體的距離r。光度和亮度的含義是不一樣的,亮度是指我們所看到的發光體有多亮，這是我們在地球上可直接測量的。光度是指發光物體本身的發光本領，關鍵是設法知道它就能得到距離。天文學家勒維特發現“造父變星”，它們的光變周期與光度之間存在著確定的關係。於是可以通過測量它的光變周期來定出光度，再求出距離。如果銀河系外的星系中有顆造父變星，那么我們就可以知道這個星系與我們之間的距離了。那些連其中有沒有造父變星都無法觀測到的更遙遠星系，當然要另外想辦法。

三角視差法和造父視差法是最常用的兩種測距方法，前一支的尺度是幾百光年，後一支是幾百萬光年。在中間地帶則使用統計方法和間接方法。最大的量天尺是哈勃定律方法，尺度達100億光年數量級。

哈勃定律方法

1929年哈勃(Edwin Hubble)對河外星系的視向速度與距離的關係進行了研究。當時只有46個河外星系的視向速度可以利用，而其中僅有24個有推算出的距離，哈勃得出了視向速度與距離之間大致的線性正比關係。現代精確觀測已證實這種線性正比關係

V = H₀×d

其中v為退行速度，d為星系距離，H₀=100h₀km·s^-1Mpc（h₀的值為0<h₀<1）為比例常數，稱為哈勃常數。這就是著名的哈勃定律。利用哈勃定律，可以先測得紅移Δν/ν通過都卜勒效應Δν/ν=V/C求出V，再求出d。

哈勃定律揭示宇宙是在不斷膨脹的。這種膨脹是一種全空間的均勻膨脹。因此，在任何一點的觀測者都會看到完全一樣的膨脹，從任何一個星系來看，一切星系都以它為中心向四面散開，越遠的星系間彼此散開的速度越大。

例子

冥王星距離太陽39.5天文單位。

木星距離太陽5.2天文單位。

參宿四的平均直徑為2.57天文單位。

月球距離地球0.0026天文單位。

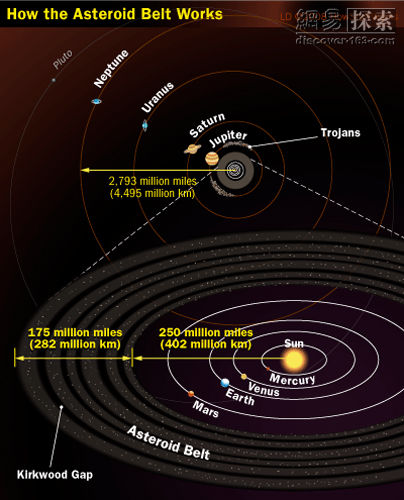
地球距離太陽1天文單位。

換算

1天文單位=1.495978707×10^11米 = 149,597,870.7公里 = 92,960,000英里 = 490,800,000,000英尺