在計算機科學中，Aho–Corasick算法是由Alfred V. Aho和Margaret J.Corasick 發明的字元串搜尋算法，用於在輸入的一串字元串中匹配有限組“字典”中的子串。它與普通字元串匹配的不同點在於同時與所有字典串進行匹配。算法均攤情況下具有近似於線性的時間複雜度，約為字元串的長度加所有匹配的數量。然而由於需要找到所有匹配數，如果每個子串互相匹配（如字典為a，aa，aaa，aaaa，輸入的字元串為aaaa），算法的時間複雜度會近似於匹配的二次函式。
基本介紹
- 中文名：AC自動機算法
- 發明人：Alfred、Margaret
簡介,樣例,
簡介
AC自動機算法主要依靠構造一個有限狀態機（類似於在一個trie樹中添加失配指針）來實現。這些額外的失配指針允許在查找字元串失敗時進行回退（例如設Trie樹的單詞cat匹配失敗，但是在Trie樹中存在另一個單詞cart，失配指針就會指向前綴ca），轉向某前綴的其他分支，免於重複匹配前綴，提高算法效率。
當一個字典串集合是已知的(例如一個計算機病毒庫), 就可以以離線方式先將自動機求出並儲存以供日後使用，在這種情況下，算法的時間複雜度為輸入字元串長度和匹配數量之和。
UNIX系統中的一個命令fgrep就是以AC自動機算法作為基礎實現的。
樣例
設一個字典中有如下單詞：{a,ab,bab,bc,bca,c,caa}.
下方的圖是用AC自動機算法由該詞典構造而成的一棵Trie樹，其中每個節點都有一條從根節點到它的路徑，代表一個單詞。
在這種數據結構中，字元串的每一個前綴都有一個節點來表示（詳見Trie）。所以如果（bca）在字典中，則會存在（bca），（bc），（b）和（）對應的節點。如果該節點表示的字元串在字典中存在，則該節點為一個藍色節點，否則為一個灰色節點。
樹中的黑色有向邊代表起點是終點的“父親”（即起點對應字元串增加一個字元可得終點對應字元串），例如從（bc）有一條指向（bca）的黑色有向邊。
樹中的藍色有向邊（後綴節點）代表終點對應字元串是起點對應字元串的最大嚴格後綴。例如對於一個節點（caa），它的嚴格後綴為（aa），（a）和（），其中在圖中且最長的為（a），所以（caa）有一條指向（a）的藍色有向邊。一個節點的藍色有向邊可以線上性時間內通過重複遍歷節點父親節點的藍色有向邊直到橫移節點（the traversing node）有一個屬於目標節點前綴的孩子。
樹中的綠色有向邊（字典後綴節點）代表終點是起點經過藍色有向邊到達的第一個藍色節點（即字典中存在終點對應字元串）。例如（bca）有一條綠色邊連向（a），因為（a）是（bca）通過藍色有向邊到達的第一個藍色節點，路徑為（bca）→（ca）→（a）。綠色有向邊也可以線上性時間內通過遍歷藍色有向邊直到找到一個藍色節點，並用記憶化的方法計算。
| 節點 | 是否在字典中 | 後綴節點（藍色有向邊） | 字典後綴節點（綠色有向邊） |
|---|---|---|---|
() | – | ||
(a) | + | () | |
(ab) | + | (b) | |
(b) | – | () | |
(ba) | – | (a) | (a) |
(bab) | + | (ab) | (ab) |
(bc) | + | (c) | (c) |
(bca) | + | (ca) | (a) |
(c) | + | () | |
(ca) | – | (a) | (a) |
(caa) | + | (a) | (a) |
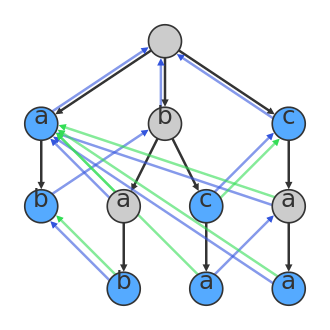一棵用AC自動機算法構造的Trie樹在每一步中，算法先查找當前節點的“孩子節點”，如果沒有找到匹配，查找它的後綴節點(suffix)的孩子，如果仍然沒有，接著查找後綴節點的後綴節點的孩子, 如此循環, 直到根結點，如果到達根節點仍沒有找到匹配則結束。
當算法查找到一個節點，則輸出所有結束在當前位置的字典項。輸出步驟為首先找到該節點的字典後綴，然後用遞歸的方式一直執行到節點沒有字典前綴為止。同時，如果該節點為一個字典節點，則輸出該節點本身。
輸入abccab後算法的執行步驟如下：
