Trie

在計算機科學中，Trie，又稱字典樹、單詞查找樹或鍵樹，是一種樹形結構，是一種哈希樹的變種。典型套用是用於統計，排序和保存大量的字元串（但不僅限於字元串），所以經常被搜尋引擎系統用於文本詞頻統計。它的優點是：利用字元串的公共前綴來減少查詢時間，最大限度地減少無謂的字元串比較，查詢效率比哈希樹高。

基本介紹

• 中文名：前綴樹或字典樹
• 外文名：Trie
• 學科：數據結構
• 別名：字典樹、單詞查找樹或鍵樹
• 定義：一種樹形結構
• 優點：查詢效率比較高

簡介

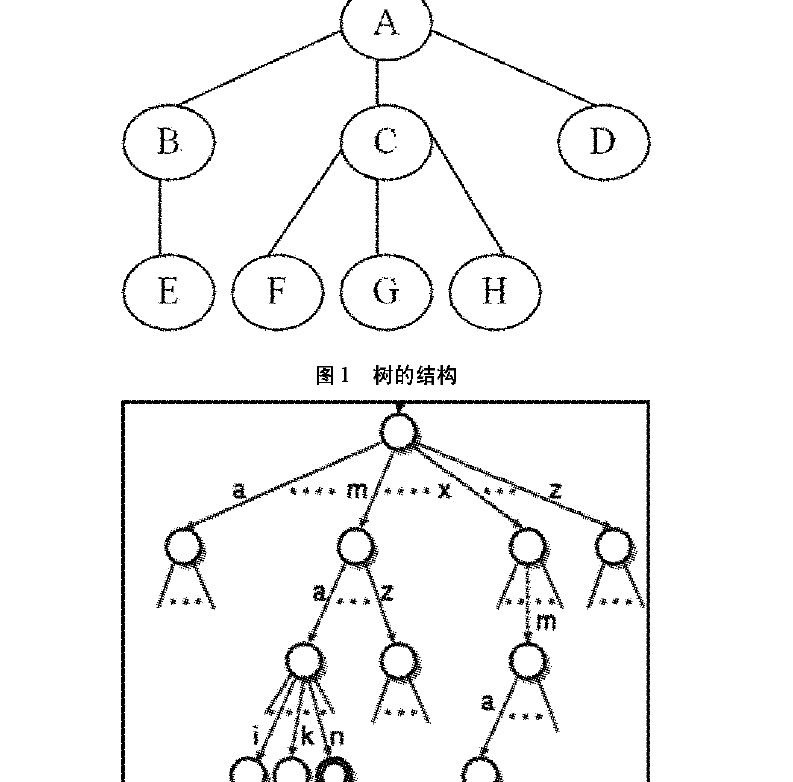
樹是數據結構中五種基本結構之一，是非線性數據結構，它是數據元素（結點）按分支關係組織起來的結構。樹結構在客觀世界中廣泛存在，如家族族譜和社會組織機構等關係都可用 樹結構形象表示。Trie是一種多叉樹，在對單詞處理中是經常利用的一種數據結構，是樹結構中一種較為特殊的樹結構，它在計算機中對字元採用鍊表方式存儲。它的某個節點不是包含一個或多個關鍵字，而是只包含組成關鍵字的一部分（字元或數字），比如：如果關鍵字是數值，則節點中只包含一個數位；如果關鍵字是單詞，則節點中只包含一個字母字元。根結點不代表任何字元，根以下第一層的結點對應於字元串的第一個字元，第二層的結點對應於字元串的第二個字元……每個字元串可由一個特殊的字元如“$”等作為字元串的結束符，用一個葉子結點來表示該特殊字元。把從根到葉子的路徑上，所有結點（除根以外）對應的字元連線起來，就得到一個字元串。因此，每個葉子結點對應一個關鍵字。在葉子結點還可以包含一個指針，指向該關鍵字所對應的元素。整個字元串集合中的字元串的數目等於葉子結點的數目。如果一個集合中的關鍵字都具有這樣的字元串特性，那么，該關鍵字集合就可採用這樣一棵鍵樹來表示。事實上，還可以賦予“字元串”更廣泛的含義，它可以是任何類型的對象組成的串。

基本性質

Trie的核心思想是空間換時間，利用字元串的公共前綴來降低查詢時間的開銷以達到提高效率的目的。它有3個基本性質：

根節點不包含字元，除根節點外每一個節點都只包含一個字元。

從根節點到某一節點，路徑上經過的字元連線起來，為該節點對應的字元串。

每個節點的所有子節點包含的字元都不相同。

套用與代碼實現

串的快速檢索

給出N個單詞組成的熟詞表，以及一篇全用小寫英文書寫的文章，請你按最早出現的順序寫出所有不在熟詞表中的生詞。

在這道題中，我們可以用數組枚舉，用哈希，用字典樹，先把熟詞建一棵樹，然後讀入文章進行比較，這種方法效率是比較高的。

“串”排序

給定N個互不相同的僅由一個單詞構成的英文名，讓你將他們按字典序從小到大輸出

用字典樹進行排序，採用數組的方式創建字典樹，這棵樹的每個結點的所有兒子很顯然地按照其字母大小排序。對這棵樹進行先序遍歷即可。

最長公共前綴

對所有串建立字典樹，對於兩個串的最長公共前綴的長度即他們所在的結點的公共祖先個數，於是，問題就轉化為當時公共祖先問題。

典樹拼法檢查算法

字典樹把要查找的關鍵字看作 一個字元序列，並根據構成關鍵字字元的先後順序構造用於檢索的樹結構。一棵n度的字典樹或者為空，或者由n棵n度的字典樹構成。 在進行查找字元的時候是按照樹結構廣度遍歷的方式來遍歷樹中每一個結點數據信息，因此，可以給出字典樹拼法檢查算法描述，如下所述：

1. 對關鍵字拼法檢查，總是在字典樹的根結點開始，且樹的根結 點為空。
2. 掃描第一層各個結點獲得查找關鍵字的第一個字元，並根據 關鍵字的第二個字元選擇對應的子樹並轉到該子樹繼續進行檢索所在 層各個結點信息，如果查找成功則轉到；否則，繼續選擇對應的子 樹進行搜尋。
3. 關鍵字的所有字元已被掃描完畢，則讀取附在該結點上的數 據信息，即完成對關鍵字的掃描過程，匹配結束。如果掃描後，沒有匹 配的字元，則匹配失敗，輸出可能字元串。

代碼實現

#define MAX 26//字元集大小typedef struct TrieNode{    int nCount;//記錄該字元出現次數    struct TrieNode* next[MAX];}TrieNode; TrieNode Memory[1000000];int allocp=0; /*初始化*/void InitTrieRoot(TrieNode* *pRoot){    *pRoot=NULL;} /*創建新結點*/TrieNode* CreateTrieNode(){    int i;    TrieNode *p;    p=&Memory[allocp++];    p->nCount=1;    for(i=0;i<MAX;i++)    {        p->next[i]=NULL;    }    return p;} /*插入*/void InsertTrie(TrieNode* *pRoot,char *s){    int i,k;    TrieNode*p;    if(!(p=*pRoot))    {        p=*pRoot=CreateTrieNode();    }    i=0;    while(s[i])    {        k=s[i++]-'a';//確定branch        if(!p->next[k])            p->next[k]=CreateTrieNode();                else            p->next[k]->nCount++;        p=p->next[k];    }} //查找int SearchTrie(TrieNode* *pRoot,char *s){    TrieNode *p;    int i,k;    if(!(p=*pRoot))    {        return0;    }    i=0;    while(s[i])    {        k=s[i++]-'a';        if(p->next[k]==NULL) return 0;        p=p->next[k];    }    return p->nCount;}