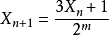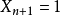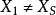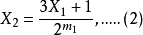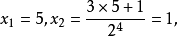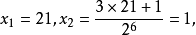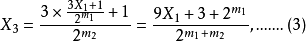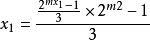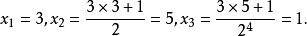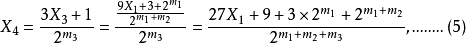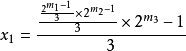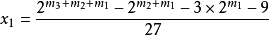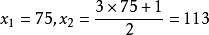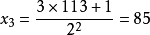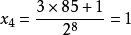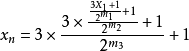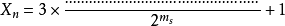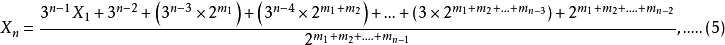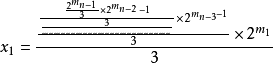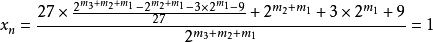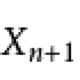所謂的3x+1猜想就是：任取一個自然數，如果它是偶數，我們就把它除以2，如果它是奇數，我們就把它乘3再加上1。在這樣一個變換下，我們就得到了一個新的自然數。如果反覆使用這個變換，我們就會得到一串自然數，猜想就是：反覆進行上述運算後，最後結果為1。
基本介紹
- 中文名：3x+1猜想
- 表達式：Xs+1=（3Xs+1）/2n
- 提出者：西拉古斯大學
- 提出時間：二十世紀五十年代
- 套用學科：初等代數
- 內容：反覆進行運算後，最後結果為1
介紹,問題由來,公式,一 這是一個依照規則的疊代公式,二 在（2）式一步到位的有,三 在（3）式二步到1的有,四 在（5）式三步到1的有,六 3x+1猜想成立是因為公式化以後,
介紹
比如說我們先取5，首先我們得到3*5+1=16，然後是16/2=8，接下去是4，2和1，由1我們又得到4，於是我們就陷在4→2→1這個循環中了。
再舉個例子，最開始的數取7，我們得到下面的序列：
7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1
這次複雜了一點，但是最終還是陷在4→2→1這個循環中。
隨便取一個其他的自然數，對它進行這一系列的變換，或遲或早，你總會掉到4→2→1這個循環中，或者說，你總會得到1。已經有人對所有小於100*2^50=112589990684262400的自然數進行驗算，無一例外。
數學裡還有嚇人的"小題"。這樣的"小題"理解起來非常容易，卻讓無數數學家大跌眼鏡，怎么冥思苦想也不得其解。3x+1問題大概就是其中最著名而又最簡單的一個。它簡單到大概任何一個會除2和會乘3的人（比如說，沒文化但是經常買菜的老奶奶）都能理解它的意思，但是困難得讓數學家沒有找到好好對付它的方法。
問題由來
這個問題大約是在二十世紀五十年代被提出來的。在西方它常被稱為西拉古斯(Syracuse)猜想，因為據說這個問題首先是在美國的西拉古斯大學被研究的；而在東方，這個問題由將它帶到日本的日本數學家角谷靜夫的名字命名，被稱作角谷猜想。除此之外它還有著一大堆其他各種各樣的名字，大概都和研究和傳播它的數學家或者地點有關的：克拉茲(Collatz)問題，哈斯(Hasse)算法問題，烏拉姆(Ulam)問題等等。在數學文獻里，大家就簡單地把它稱作"3x+1問題"。
角谷靜夫在談到這個猜想的歷史時講："一個月里，耶魯大學的所有人都著力於解決這個問題，毫無結果。同樣的事情好象也在芝加哥大學發生了。有人猜想，這個問題是蘇聯克格勃的陰謀，目的是要阻礙美國數學的發展。"不過我對克格勃有如此遠大的數學眼光表示懷疑。這種形式如此簡單，解決起來卻又如此困難的問題，實在是可遇而不可求。
數學家們已經發表了不少篇嚴肅的關於3x+1問題的數論論文，對這個問題進行了各方面的探討，在後面我會對這些進展作一些介紹。可是這個問題的本身始終沒有被解決，我們還是不知道，"到底是不是總會得到1？"
在1996年B. Thwaites懸賞1100英鎊來解決這個問題。我寫一下這個懸賞的文獻：Thwaites, B. "Two Conjectures, or How to win ￡1100."Math.Gaz. 80, 35-36, 1996，好在大家萬一證出來時知道跑哪裡去領獎。看在錢大爺的份上，3x+1問題於是又多了個名字，叫Thwaites猜想。
公式
一 這是一個依照規則的疊代公式
：
...........（1）
X是奇數，m是使得3X+1中的偶數析出並且抵消讓整個分數成為奇數。這是一個疊代公式，如果
，就結束，如果是奇數，就代入公式繼續進行，直到等於1為止。
證明這個猜想需要證明兩點：
1，公式中X不會循環，就是
，s>1。
2，公式中的數值不會發散。
第1點容易證明，只要把公式（1）展開即可得到。
二 在（2）式一步到位的有
5， 21， 85， 341，1365， 5461， 21845， .....。
例如：
..............。
三 在（3）式二步到1的有
（3）式反推二步到位的
形的數：3，13，53， 113， 227， 909，....。
例如：
四 在（5）式三步到1的有
在（5）式反推三步到位的
.......(6)
（6）式簡化：
形的數：11，17， 75，301，1205，...。
例如：
六 3x+1猜想成立是因為公式化以後
分子分母抵消
對於任意n：
簡化以後：
(8)
對於任意n，
(9)式代入（10）式，剛好分子與分母抵消。
例如，（6-1）式代入（5）式：
分子與分母剛剛抵消。
有了公式，這個猜想進入理論化。
------------------------
要是真的有這么一個自然數，對它反覆作上面所說的變換，而我們永遠也得不到1，那只可能有兩種情況。
1)它掉到另一個有別於4→2→1的循環中去了。我們在後面可以看到，要是真存在這種情況，這樣一個循環中的數字，和這個循環的長度，都會是非常巨大的；
2)不存在循環。也就是說，每次變換的結果都和以前所得到的所有結果不同。這樣我們得到的結果就會越來越大（當然其中也有可能有暫時減小的現象，但是總趨勢是所得的結果趨向無窮大）。
3x+1問題算法的c語言編程，其實很簡單，初學c語言的學生也能明白：
#include<stdio.h>
long main()
{
long x,i,t;
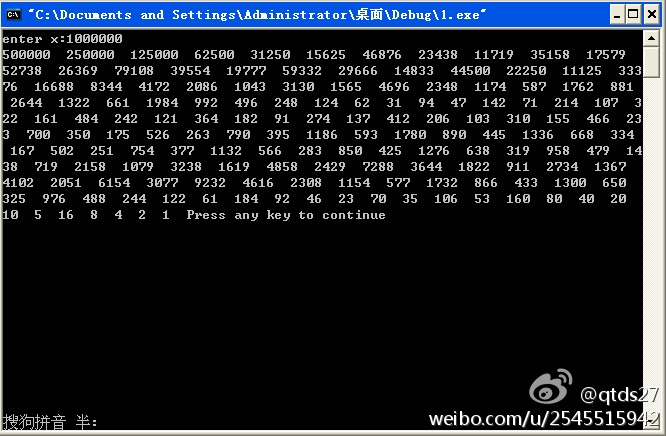
printf("enter x:");
scanf("%d",&x);
do
{
if(x%2==0)
i=x/2;
else
i=3*x+1;
printf("%d ",i);
x=i;
}
while(x!=1);
return 0;
}
如圖所示為1百萬的執行結果：
