黑利定理(Helly theorem)是凸集交叉處離散幾何的基本結果。 它是由愛德華·赫利於1913年發現的,但直到1923年才被他發表,當時Radon(1921年)和König(1922年)的替代證明已經出現。 Helly定理引出了Helly家族的概念。
基本介紹
- 中文名:黑利定理
- 外文名:Helly theorem
定義,證明,
定義
設 ,...,
,..., 是
是 的凸子集的有限集合,其中
的凸子集的有限集合,其中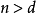 。如果這些集合中每個
。如果這些集合中每個 的交集是非空的,則整個集合具有非空交集;那是,
的交集是非空的,則整個集合具有非空交集;那是,



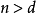

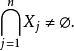
設{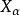 }是
}是 的緊緻凸子集的集合,使得基數最多
的緊緻凸子集的集合,使得基數最多 的每個子集合都具有非空交集。然後整個集合都有非空的交集。
的每個子集合都具有非空交集。然後整個集合都有非空的交集。
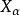


證明
我們使用Radon定理證明了有限形式,如Radon(1921)的證明。然後無限版通過緊緻性的有限交集屬性表征:若且唯若每個有限子集合具有非空交集時,緊湊空間的閉合子集的集合具有非空交集(一旦您修復單個集合,所有其他人與它的交集是固定緊湊空間的封閉子集。
證據是通過歸納:
基本情況:設 。根據我們的假設,對於每個j = 1,...,n,存在一個點
。根據我們的假設,對於每個j = 1,...,n,存在一個點 ,它位於所有
,它位於所有 的公共交叉點中,可能是
的公共交叉點中,可能是 的例外。我們將Radon定理套用於集合A = {
的例外。我們將Radon定理套用於集合A = {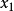 ,...,
,...,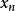 },它為我們提供A的不相交子集
},它為我們提供A的不相交子集 ,
, ,使得
,使得 的凸包與
的凸包與 的凸包相交。假設p是這兩個凸包的交點中的一個點。我們聲稱:
的凸包相交。假設p是這兩個凸包的交點中的一個點。我們聲稱:




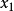
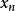




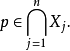





















上面,我們假設點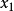 ,...,
,...,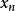 都是不同的。如果不是這種情況,比如對於某些
都是不同的。如果不是這種情況,比如對於某些 ,則說
,則說 =
= ,則
,則 在每個集合
在每個集合 中,並且我們再次得出結論交集是非空的。這樣就完成了
中,並且我們再次得出結論交集是非空的。這樣就完成了 的證明。
的證明。
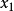
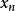






歸納步驟:假設 ,並且該陳述對於n-1為真。上面的論點表明,
,並且該陳述對於n-1為真。上面的論點表明, 集的任何子集合都將具有非空交集。然後我們可以考慮使用單組
集的任何子集合都將具有非空交集。然後我們可以考慮使用單組 ∩
∩ 替換兩組
替換兩組 和
和 的集合。在這個新集合中,
的集合。在這個新集合中, 集的每個子集合都將具有非空交集。因此,歸納假設適用,並表明這個新集合具有非空交集。這意味著原始集合相同,並完成證明。
集的每個子集合都將具有非空交集。因此,歸納假設適用,並表明這個新集合具有非空交集。這意味著原始集合相同,並完成證明。







