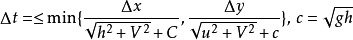麥科馬克格式(MacCormack Scheme)是一種解可壓縮流體流動問題的二步二階差分格式。它可看做拉克斯-溫德洛夫格式的預估-校正形式，在兩步中交替使用向前和向後差分。由於此格式簡單，要求計算機記憶體少，已普遍地套用於氣動問題的計算。
基本介紹
- 中文名：麥科馬克格式
- 外文名：MacCormack Scheme
- 領域：數理科學
- 學科：計算數學
- 套用：氣動問題
- 相關：差分方法、Lax-Wendroff格式
定義,性質,套用示例——河道流速計算,二維淺水方程,水流控制方程,方程求解,邊界條件,穩定條件,意義,
定義
麥科馬克格式(MacCormack Scheme)是一種解可壓縮流體流動問題的二步二階差分格式。它可看做拉克斯-溫德洛夫格式(Lax-Wendorff Scheme)的預估-校正形式，在兩步中交替使用向前和向後差分。
對一階雙曲型偏微分方程
，麥科馬克格式為：
式中
和
分別為時間和空間步長，
其他量類似。
該格式在計算中分為兩步，即預測步和校正步，第一步用向前差分，第二步用向後差分；也可以反過來，即第一步用向後差分，第二步用向前差分。對於二維問題，可在x和y方向不同地用向前/向後差分，且在二個或四個完整的時間步上循環地套用。由於此格式簡單，要求計算機記憶體少，已普遍地套用於氣動問題的計算。
該格式是麥科馬克(MacCormack,R.W)於1969年發表的。
性質
MacCormack格式是一個相容的二階精度格式，是Lax-Wendorff兩步格式的變形，適用於非線性方程的離散，是在流體力學中廣泛套用的一種格式。
優點：比Lax-Wendorff格式簡單，不需要計算函式在半點上的值；
缺點：定常解的誤差依賴於時間步長。
套用示例——河道流速計算
二維淺水方程
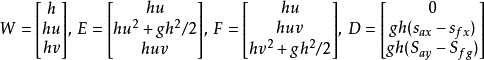
其中，u, v分別是x, y方向的平均速度；h是水深；t是時間；g是重力加速度；
分別是x, y方向的河底坡降；
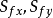分別是x, y的摩阻坡降；
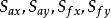的計算式分別是：
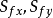
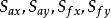
式中，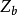
是河底高程；n是曼寧糙率。
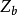
水流控制方程
採用九結點四邊形等參元函式將物理平面的任意四邊形單元變換成計算平面上規則的矩形單元，然後在汁算平面上求解變換後的水流控制方程。這樣，物理平面上（如圖1(a)所示x-y坐標系）的流場要素就反映到計算平面上（圖1(b)所示ξ-η坐標系），具體變換如下：
在圖1所示的單元上作局部坐標變換：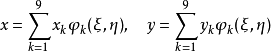
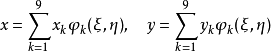
圖1 局部坐標變換
圖1 局部坐標變換式中
為單元結點在x-y坐標系中的坐標；
為形函式，具體表達式為：
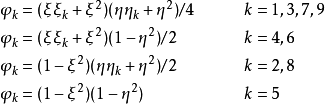
該變換將圖1(a)的任意四邊形變成規則矩形，圖1(b)所示。
如果用H表示從物理平面到計算平面的變換矩陣，則有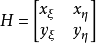
，雅可比行列式的形式是：
，式中，x, y對ξ, η的導數分別是：
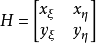
由微分法則可以推出：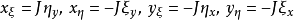
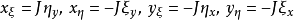
根據以上的變換，新坐標系ξ-η下的水流控制方程是：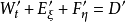
，這裡，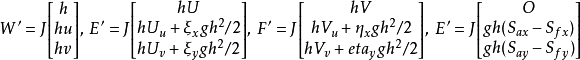
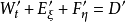
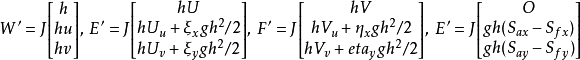
其中，U, V是新坐標系下ξ, η方向的速度，u, v和U, V的轉換關係是：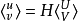
。
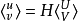
方程求解
採用MacCormack格式離散求解變換後的水流控制方程如下：
根據該方程可以計算出h, u, v的預測值。
