鮑克斯-詹金斯方法又稱ARIMA方法,研究的是有關隨機性時間序列變動趨勢的預測。它認為:除去純偶然因素引起的個別序列值以外,時間序列是依賴於時間t的一族隨機變數,儘管單個序列值的出現具有不確定性,但整個序列的變化卻呈現一定的規律性。鮑克斯-詹金斯方法(Box-Jeknins)是時間序列分析方法中較為常用的一種方法,該方法假設各變數之間是一種線性關係(或擬線性關係)。但在處理一些複雜曲線問題時,這種局限性使其在實際套用過程中很難準確地進行分析和預測。為了解決這個問題,在過去的十多年中,一些學者提出了適用於非線性時間序列的分析、預測方法。如H.Tong於1978年提出的門限自回歸模型等,即首先辨識出各數據間的關係,然後再估計模型參數。
基本介紹
- 中文名:鮑克斯-詹金斯方法
- 外文名:Box—Jenkins method
- 別名:ARIMA方法、B-J方法等
- 提出者:G·鮑克斯和G·詹金斯
- 所屬學科:數學
- 所屬問題:統計學(時間序列分析)
基本介紹,鮑克斯-詹金斯法中的模型簡介,模型分析工具,散點圖,自相關係數,偏自相關係數,線譜分析,鮑克斯-詹金斯方法的特點,套用步驟,鮑克斯-詹金斯方法的局限性,
基本介紹
鮑克斯-詹金斯方法(Box-Jenkins)由G·鮑克斯和G·詹金斯1976年在其著作中闡明。是分析時間序列的一種有效的方法。這種方法通常用於短期預測。它能夠在事先對數據模式未知的情況下,找到適合考察數據的模型。在經濟計量學中三種預測方法:時間序列分析、回歸分析和多方程模型分析中,鮑克斯-詹金斯方法雖然在原則上屬於第一種類型,但同時融和了第二類方法的某些原理,因而被認為是在前兩種方法的基礎上發展起來的一種高級的經濟預測手段。在常見的事件序列分析中,各類被解釋變數歷史統計數據的變化有不同的特點。當數據變化具有明顯的周期性,循環性和規律性時,稱這種時間序列分析為確定性時間序列分析,反之則稱其為隨機性時間序列分析。確定性時序分析模型計算簡便,但預測的準確性較差,隨機性時序分析模型計算比較複雜,但預測的準確性明顯高於前者。鮑克斯-詹金斯分析法研究的,是有關變數隨機性時間序列變動趨勢的預測。它所採用的數學模型亦屬於隨機性時序分析模型。
鮑克斯-詹金斯法中的模型簡介
鮑克斯-詹金斯分析法包含的經濟計量模型,具體說來有三種:自回歸模型,簡稱AR模型;移動平均模型,簡稱MA模型;組合的自回歸移動平均,簡稱ARIMA模型。AR模型描述不同周朗內被解釋變數的隨機寸序之間的關聯程度.並以變數的滯後時間數列為依據推算其未來的時間數列。
①一般的p階AR模型方程式為:
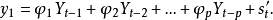
式中 =t期預測值,
=t期預測值,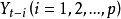 =過去t-i期觀察值,
=過去t-i期觀察值,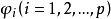 ,過去i期自回歸係數,
,過去i期自回歸係數,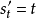 期預測誤差。
期預測誤差。

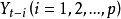
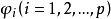
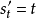
②MA模型反映一定時期內被結束變數的隨機時序平均水平的變化趨勢,並根據過去的誤差項推測變數未來的時序。—般的q階MA模型的方程式為:
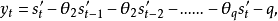


③ARIMA模型是上兩種模的組合,它可以更全面地描述和預測自變數的變化規律與趨勢。這種組合又可分為兩種形式。當時間數列具有平穩性特徵時,它選擇混合模型(ARMA),當數列具有齊次非穩定性特徵時,它採用結合模型(ARIMA)。該模型與前者的區別在於需先對原數列做差分處理,使其變為穩定序列。養分後的時間數列表示為: ,式中
,式中 為差分符號,d代表差分的階數。
為差分符號,d代表差分的階數。


模型分析工具
散點圖
以時間為橫坐標,時間序列組為縱坐標,從中可以直觀地了解數據的一些大致趨向。
自相關係數
自相關係數 ,表征時間序列
,表征時間序列 的相關程度,其取值範圍為:-1≤
的相關程度,其取值範圍為:-1≤ ≤+1,其絕對值越接近於1,表明序列自相關越高。定義為:
≤+1,其絕對值越接近於1,表明序列自相關越高。定義為:




其中,

n—— 樣本數據個數;
k——滯後期
偏自相關係數
偏自相關係數 ,它是時間序列
,它是時間序列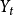 在給定
在給定 的條件下,
的條件下,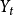 與
與 之間的條件相關程度,定義為:
之間的條件相關程度,定義為:

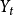

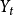

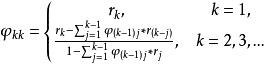
線譜分析
線譜分析即用正弦函式來分析時間序列的隨機性、季節性和自相關狀況。用正弦函式去描述- -個時間序列時,其公式為:
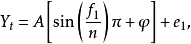


n、f——已知量;
A、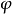 待定係數。
待定係數。
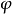
鮑克斯-詹金斯方法的特點
鮑克斯-詹金斯分析方法具有5個特點:
①作為一種時序分析法,它需要大量的歷史數據資料支持,觀察值通常應有50~100項。
①作為一種隨機性模型分析法,它假定不論過去、現在和將來,時間序列的結構不變,即時序具有穩定性。對於不穩定的數列則必須進行差分處理。
③它不研究變數之間的因果關係,而是根據某種變數過去變化的統計規律,大體推測出其未來變化趨勢。變數的時間序列間隔越小,期限越短,模型預測結果的精度相對說來越高。因而,它主要適用於短期預測。
⑤這種分析法的模型體系數學演算工作量很大,因此在實際上套用過程中必須藉助於計算機。目前流行的許多有關的微機軟體對此提供了很大的幫助。
套用步驟
利用鮑克斯-詹金斯方法進行預測,預測模型的建立,大體分為5個步驟:
①對模型的識別。
②對模型的選擇。在AR模型、MA模型和ARIMA模型中加以選擇。
②模型的檢驗,檢驗有兩種含義,一是對初步選定的三種模型的運算結果進行統計檢驗,二是對不同模型的檢驗值進行比較,從中選出最佳者用於預測。
④對模型的修正。
⑤預測趨勢。
鮑克斯-詹金斯方法的局限性
鮑克斯-詹金斯分析方法作為一種短期預測的定量分析工具,在實際套用方面效果比較理想。但這種方法亦有其局限性:①由於它必須以大量的、系統的所史數據為基礎建立模型,所以,對於那些統計資料不完整或形成時期不長的經常變數的預測來說,此方法愛莫能助。②它假定自變數的時序是個平穩系列,即不論過去、現在和將來,序列的結構或發展模式不變,這與現實不符。為此,我們不可能始終使用原始模型更新預測內容。換言之,隨著時間的推移,使用者必須不斷地根據新的時序資料重新擬合模型,以期做出新的預測。
任何一種經濟預測方法均有長處和缺憾,鮑克斯-詹金斯分析法自然也不會例外。在實踐中我們應當充分認識到這一點,注意將多種預測方法結合起來,以此之長補彼之短,使預測工作的質量不斷提高。

