高階奇點托姆定義是高階奇點的一種定義,是對一階奇點進一步分類的一種方法。在一階奇點分類不足以充分刻畫其性質時可做更細微的分類方法。
基本介紹
- 中文名:高階奇點的托姆定義
- 外文名:higher order singularities , the definition of Thom
- 適用範圍:數理科學
簡介,托姆構想,
簡介
高階奇點托姆定義是高階奇點的一種定義,對一階奇點進一步分類的一種方法。在一階奇點分類不足以充分刻畫其性質時可做更細微的分類方法,奇點的 分類(即一階奇點)還不夠精細,映射在兩個同一類型
分類(即一階奇點)還不夠精細,映射在兩個同一類型 的奇點上,可能具有極不同的性態。因此有必要對奇點做進一步的分類,托姆(Thom,R.)提出了一個構想。
的奇點上,可能具有極不同的性態。因此有必要對奇點做進一步的分類,托姆(Thom,R.)提出了一個構想。


托姆構想
先從一個具體的例子來看托姆的思想,考慮映射f如下:


f 的雅可比矩陣為





拋物線 是 R上的光滑曲線,因此可以考慮 f 在
是 R上的光滑曲線,因此可以考慮 f 在 上的限制映射
上的限制映射 ,此時,原點是
,此時,原點是 的
的 型奇點,奇點集
型奇點,奇點集 記為
記為 。拋物線
。拋物線 除原點外其他點皆為
除原點外其他點皆為 型奇點,奇點集
型奇點,奇點集 記為
記為 。
。











這樣就把 f 的奇點集 進一步分為兩類奇點
進一步分為兩類奇點 和
和 。
。



對一般情況,托姆的構想如下:設 f:M→N 是光滑映射,若奇點集 是 M 的子流形,則可以考慮 f 在
是 M 的子流形,則可以考慮 f 在 上的限制映射
上的限制映射 的
的 型奇點集記為
型奇點集記為 ,即
,即 ,稱為 f 的
,稱為 f 的 型奇點,這是二階奇點,若
型奇點,這是二階奇點,若 還是 M 的子流形,則可以仿照上述構造三階奇點
還是 M 的子流形,則可以仿照上述構造三階奇點









最一般的情形,可以歸納構造如下:對於任意非負整數集 ,若
,若







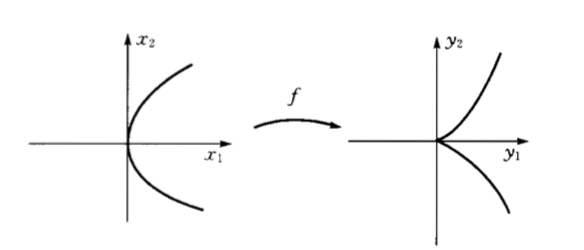 圖1.
圖1.