高斯-克呂格投影是由德國數學家、物理學家、天文學家高斯於19世紀20年代擬定,後經德國大地測量學家克呂格於1912年對投影公式加以補充,故稱為高斯-克呂格投影,又名"等角橫切橢圓柱投影”,是地球橢球面和平面間正形投影的一種。
基本介紹
- 中文名:高斯-克呂格投影
- 外文名:Gauss -Krugerprojection
- 提出者:高斯
- 提出時間:19 世紀20 年代
- 適用領域:地圖測繪
- 套用學科:地理信息
- 完善者:克呂格
幾何概念
基本概念
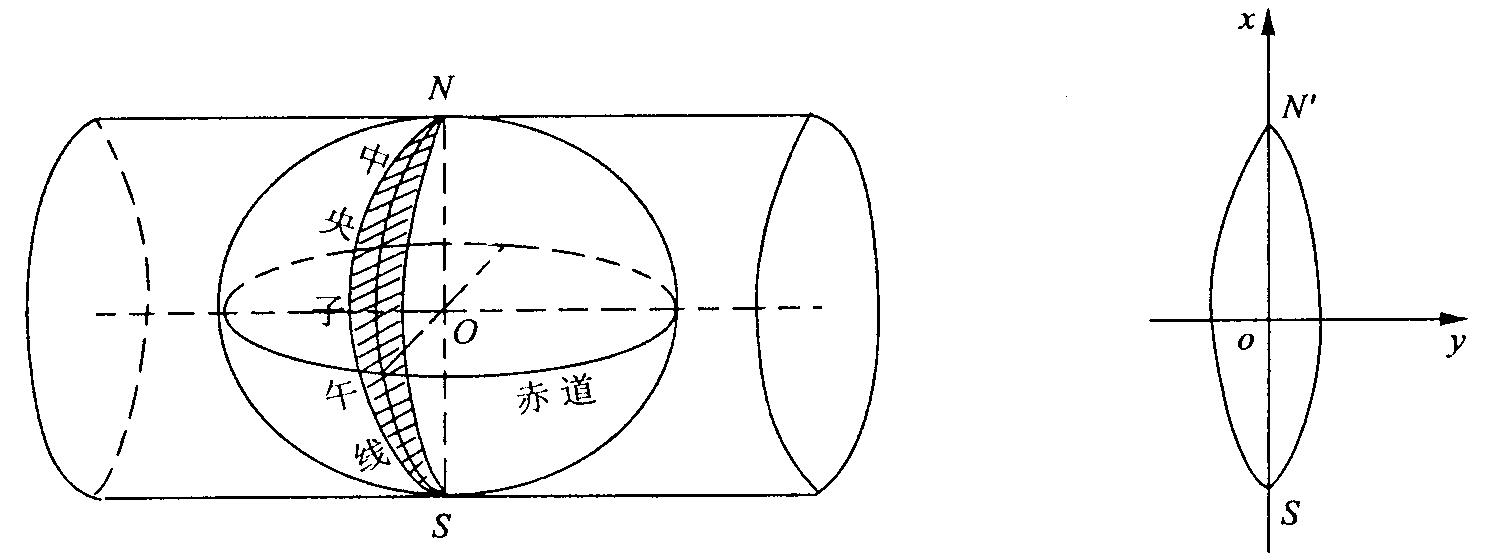

橢球面三角系
高斯-克呂格投影是由德國數學家、物理學家、天文學家高斯於19世紀20年代擬定,後經德國大地測量學家克呂格於1912年對投影公式加以補充,故稱為高斯-克呂格投影,又名"等角橫切橢圓柱投影”,是地球橢球面和平面間正形投影的一種。




高斯克呂格投影( Gauss.Krueger Projection),是一種等角橫切橢圓柱投影。其投影帶中央子午線投影成直線且長度不變,赤道投影也為直線,並與中央子午線正交。為了方便工程的規劃、設計與施工,我們需要把測區投影到平面上來,使測量計算和繪圖更加方便。而地理坐標是球面坐標,當測區範圍較大時,要建平面坐標系就不...
由於用高斯-克呂格投影每個投影帶都有一個獨立的高斯平面直角坐標系,則位於兩個不同投影帶的地圖點會出現具有相同的高斯平面直角坐標,而實際上描述的卻不是一個地理空間。為了便於地形圖的量測作業,在高斯――克呂格投影帶內布置了平面直角坐標系統。具體構成是: 規定以中央經線為X軸,赤道為Y軸,中央經線與...
把地球上的點位化算到平面上,稱為地圖投影。地圖投影的方法有很多,我國採用的是高斯——克呂格投影(又稱高斯正形投影),簡稱高斯投影。它是由德國數學家高斯提出的,由克呂格改進的一種分帶投影方法。它成功解決了將橢球面轉換為平面的問題。投影方法 高斯投影的方法是將地球按經線劃分為帶,稱為投影帶。投影...
高斯地圖投影(Gauss map projection)是2012年公布的地理信息系統名詞,出自《地理信息系統名詞》第二版。定義 一種等角橫切橢圓柱投影。由德國數學家、天文學家高斯(G. F. Gauss)擬定,德國大地測量學家克呂格(J. Krüger)補充而成。假想用一個橢圓柱橫切於橢球面上投影帶的中央子午線,將中央子午線兩側一定經差...
高斯(Gauss)投影是橫切橢圓柱等角投影,最早由德國數學家高斯提出,後經德國大地測量學家克呂格完善、補充並推導出計算公式,故也稱為高斯-克呂格投影。高斯投影是一種數學投影,而不是透視投影。高斯投影的條件為:1.投影后沒有角度變形;2.中央子午線的投影是一條直線,並且是投影點的對稱軸;3.中央子午線的投影...
常用的投影方法有墨卡托投影(正軸等角圓柱投影)、高斯-克呂格投影、斜軸等面積方位投影、雙標準緯線等角圓錐投影、等差分緯線多圓錐投影、正軸方位投影等。基本方法 幾何透視法 幾何透視法是利用透視的關係,將地球體面上的點投影到投影面(藉助的幾何面)上的一種投影方法。如假設地球按比例縮小成一個透明的地球儀...
約翰·海因里希·路易斯·克呂格 克呂格(Johann Heinrich Louis Krüger,1857年9月21日-1923年6月1日),德國數學家和大地測量學家。他於1912年推導出簡單實用的坐標投影公式,使得高斯-克呂格坐標系得以廣泛套用。地圖學 地圖學(英語:Cartography;希臘語:χάρτης [Chartisgraphein],即為英文的Map...
高斯平面坐標 高斯平面坐標是2012年公布的地理信息系統名詞。 定義 利用高斯-克呂格投影,以中央子午線為縱軸、赤道投影為橫軸所構成的平面直角坐標系。 出處 《地理信息系統名詞》。
蘭勃特—高斯投影”。圓柱投影面與中央經線相切的一種等角投影。verse Mercato projection 這種投影圖上,中央經線為直經,其它經緯線為對稱於中央經線的曲線,中央經線為標準線,等變形線與中央經線平行,離中央經線越遠則變形越大。此投影是將地球當作半徑為R的球體,若將地球作為橢球時,便是高斯—克呂格投影。
由此可見,一個直角在不同的位置下的投影有著不同的的大小,可以由銳角變為鈍角,或者相反。那么在變化的過程中,必然有一特殊位置,直角投影后仍保持直交,此二直交直線方向,稱之為主方向。在主方向上,具有極大和極小長度比。例如我們講過的高斯-克呂格投影,經緯線投影后均保持垂直。所以該投影中,經緯線...
高斯-克呂格(GAUSS-KRUGER)是等角橫切橢圓柱投影,是橫軸墨卡托投影的變種。該詞主要出現於地圖投影中。由德國數學家高斯提出,後經克呂格擴充並推倒出計算公式,故稱為高斯-克呂格投影,簡稱高斯投影。該投影以中央經線和赤道投影后為坐標軸,中央經線和赤道交點為坐標原點,縱坐標由坐標原點向北為正,向南為負,...
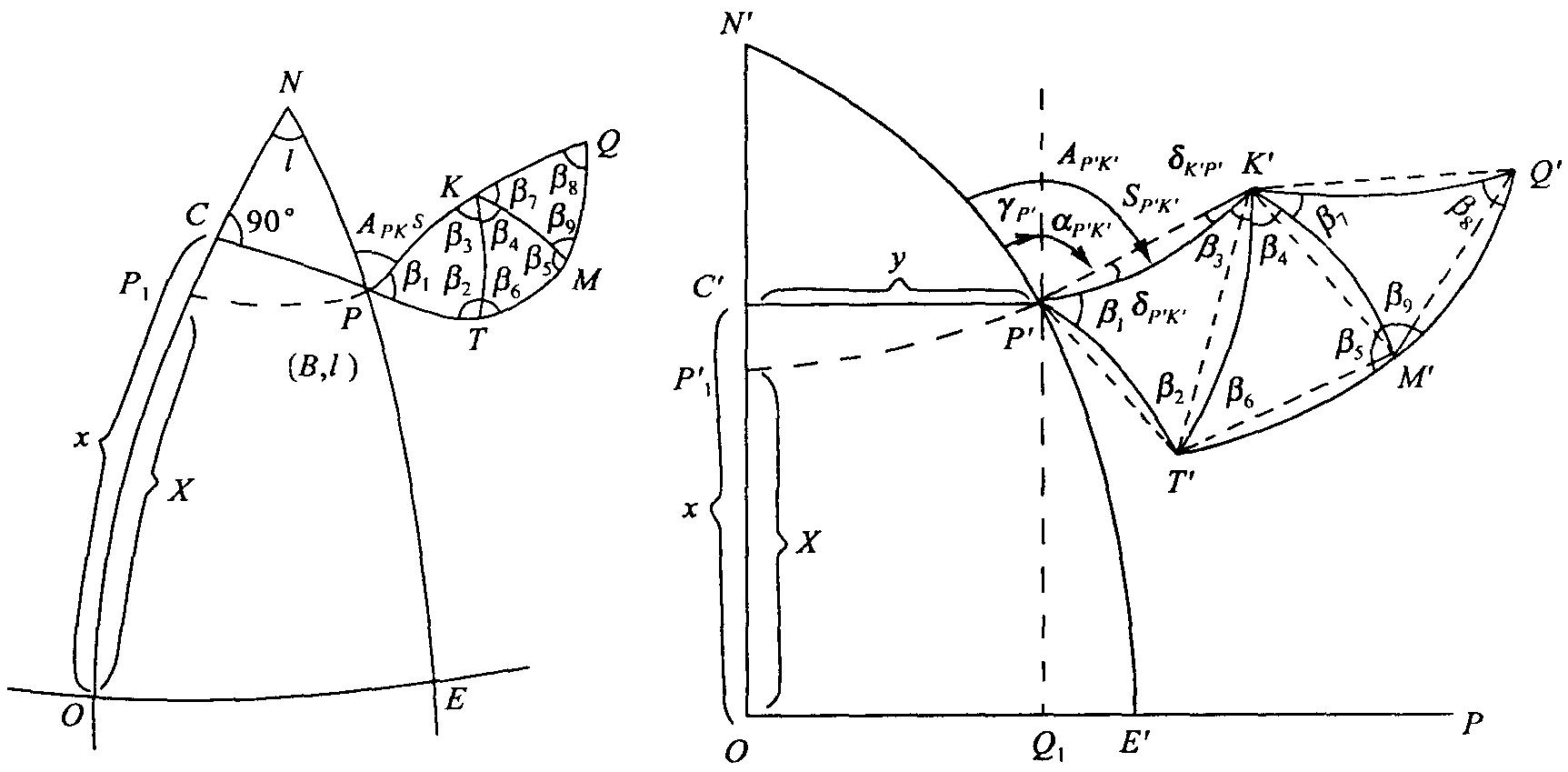
高斯-克呂格平面直角坐標系 根據高斯-克呂格投影所建立的平面坐標系,簡稱高斯平面坐標系。它是大地測量、工程測量和地圖製圖中廣泛採用的一種平面坐標系。高斯-克呂格投影 大地測量成果,即大地坐標(L,B),不能滿足地形測圖和各種工程測量的要求,需將它們按一定的數據關係轉換為平面直角坐標。1882年,德國著名...
高斯-克呂格(Gauss-Kruger)投影簡稱“高斯投影”,又名"等角橫切橢圓柱投影”,地球橢球面和平面間正形投影的一種。德國數學家、物理學家、天文學家高斯(Carl FriedrichGauss,1777一 1855)於十九世紀二十年代擬定,後經德國大地測量學家克呂格(Johannes Kruger,1857~1928)於 1912年對投影公式加以補充,故名。
在高斯-克呂格投影中,北向距離從赤道起算。與之相反,為了避免負值,UTM在南半球增加10000公里。距離中央經線的距離,與高斯-克呂格投影一樣,要偏移500公里。相應的坐標以E(東)和N(北)標明。中央經線分別為3°,9°,15°等等。南、北極點間的區域被分成8個維度帶,並以字母標示。該系統用於美國和NATO的...
表示點的平面位置。中國一般採用以高斯-克呂格投影分帶的中央子午線為縱軸和赤道的投影為橫軸的高斯-克呂格平面直角坐標系,簡稱高斯平面坐標系。坐標縱軸為x,自原點向北為正;坐標橫軸為y,自原點向東為正。點的平面坐標為(x,y)。平面坐標是1954年為了開展我國的測繪事業而建立的學科。定義 定義一 坐標縱軸為x,自...
東偽偏移 falseEasting falEastng是投影平面中為避免橫軸(經度方向)坐標出現負值,而所加的偏移量。我國規定將高斯-克呂格投影各帶縱坐標軸西移500公里,因此高斯-克呂格投影東偽偏移值為500公里。如:500000,表示投影的東偽偏移值為500公里 。北偽偏移 falseNorthing falNorthng :投影平面中為避免縱軸(緯度方向)...
北京54和西安80是我們使用最多的坐標系,在ArcGIS檔案中,對於這兩種坐標系統的命名有一些不同,我國大中比例尺地圖均採用高斯-克呂格投影,其通常是按6度和3度分帶投影,1:2.5萬-1:50萬比例尺地形圖採用經差6度分帶,1:1萬比例尺的地形圖採用經差3度分帶。具體分帶法是:6度分帶從本初子午線開始,按...
為了製作和使用地圖的方便,高斯-克呂格投影的地圖上繪有兩種坐標網:地理坐標網和直角坐標網。基本信息 在我國1:1萬-1:10萬地形圖上,經緯線只以圖廓的形式表現,經緯度數值註記在內圖廓的四角,在內外圖廓間,繪有黑白相間或僅用短線表示經差、緯差1’的分度帶,需要時將對應點相連線,就構成很密的...
北京坐標系 “北京2000坐標系”是經自然資源部批准的北京市唯一合法的相對獨立的平面坐標系統。釋義 該系統採用高斯-克呂格投影,以東經116°23′28″作為中央子午線,坐標系統原點位於東經116°23′28″與北緯39°54′22″的交點,投影面高程為0米。
對於這兩種坐標系統的命名有一些不同,簡單看去很容易讓人產生迷惑。在此之前,先簡單介紹高斯-克呂格投影的基本知識,了解就直接跳過,我國大中比例尺地圖均採用高斯-克呂格投影,其通常是按6度和3度分帶投影,1:2.5萬-1:50萬比例尺地形圖採用經差6度分帶,1:1萬比例尺的地形圖採用經差3度分帶。
眼下我國採用的空間格線系統就是世界通用的經緯度網和國家測繪地理信息局公布的基於高斯一克呂格投影的直角坐標網。一切地理空間數據的採集、分析、分級、檢索、表示、歸檔都受此國家標準的約束。隨著遙感技術的進步和網路環境的便捷套用,地理空間數據量空前增加,及時處理這些數據也會涉及地球表而剖分等算法的套用。近...
1:1萬地形圖主要用於小範圍內詳細研究和評價地形,城市、鄉鎮、農村、礦山建設的規劃、設計,林斑調查,地籍調查,大比例尺的地質測量和普查,水電等工程的勘察、規劃、設計,科學研究,國防建設的特殊需要,以及可作為編制更小比例尺地形圖或專題地圖的基礎資料。投影方式 1:1萬地形圖採用高斯—克呂格投影,3°分...
允差分析法,又稱調整距離法。是通過誤差分析分別控制投影變形計算公式兩分項的變形限差,調整放線距離來控制投影變形的方法,距離調整公式為Δd =H/6.37-C(以mm/km計)。允差分析法根據線路里程範圍內各變形檢查點因高斯-克呂格投影產生的變形值,分析出滿足限差要求的常數C,在全里程範圍內採用;再讀取每公里...
平面直角坐標 用平面上的長度值表示地面用平面上的長度值表示地麵點位置的直角坐標。點位置的直角坐標。中華人民共和國地形圖採用高斯-克呂格投影建立平面直角坐標系。地形圖上坐標值均以千米數為單位,註記在內外圖廓線之間。平面直角坐標,計算簡便。軍事上用以指示和確定目標在圖上的位置,量算距離和面積。
地面測量坐標系通常是指空間大地坐標基準下的高斯-克呂格6帶或3%帶(或任意帶)投影的平面直角坐標(例如1954年北京坐標系或1980西安大地坐標系)與定義的從某一基準面量起的高程(例如1956 年黃海高程或1985 年國家基準高程),兩者組合而成的空間左手直角坐標系。地面測量坐標系通常是指空間大地坐標基準下的高斯-克呂格...
高斯平面直角坐標系 為了方便工程的規劃、設計與施工,我們需要把測區投影到平面上來,使測量計算和繪圖更加方便。而地理坐標是球面坐標,當測區範圍較大時,要建平面坐標系就不能忽略地球曲率的影響。把地球上的點位化算到平面上,稱為地圖投影。地圖投影的方法有很多,我國採用的是高斯——克呂格投影(又稱高斯正...
由於地圖投影有不同程度的變形,比例尺隨著線段的地理位置和方向的不同而不同。圖上標明的比例尺,只是某一條經線或緯線上的比例尺,這個比例尺稱為主比例尺,它只是在某條經線或緯線上是正確的。如高斯——克呂格投影的中央經線、墨卡托投影的基準緯線。圖上其他部位的比例尺均大於或小於主比例尺,它們被稱為...
地理坐標系是用於確定點在地球上位置的坐標系。某一特定的地理坐標系是由一個特定的橢球體和一種特定的地圖投影構成。絕大多數的地圖都是遵照一種已知的地理坐標系來顯示坐標數據。例如,我國1:25 萬地形圖,其橢球體採用的是1975 年國際大地測量協會推薦的參考橢球體,而投影是高斯一克呂格投影。經緯度坐標系是...
