高斯記號

數學上，高斯記號（Gauss mark）是指對取整符號和取小符號的統稱，用於數論等領域。

基本介紹

• 中文名：高斯記號
• 外文名：Gauss Mark
• 表達式：y=[x]或y={x}
• 領域：數學

定義

在數學特別是數論領域中，有時需要略去一個實數的小數部分只研究它的整數部分，或需要略去整數部分研究小數部分，因而引入高斯記號。

• 設x∈R，用 [x]或int(x)表示不超過x的最大整數。也可記作⌊x⌋。
  
• 設x∈R，用 {x}表示x的非負純小數（Gauss mark），即{x}=x－[x]。
  

舉例

• [1]=1；[0]=0；[－1]=－1。
  
• [－1.2]=－2；[－3]=－3。
  
• {1.5}=0.5；{－1.5}=0.5；{－1.2}=0.8。
  

注意

1. 負實數，例如 ，要特別注意 ≠－0.25， ≠0.25。按照定義， =0.75。

2. 注意高斯記號的符號不要與算式中的中括弧、大括弧搞混。

性質

• 對於任意實數x，x=[x]+{x}；
  
• x－1<[x]≤x<[x]+1；
  
• [n+x]=n+[x]，n為整數；
  
• f(x)=[x]是不減函式；
  
• f(x)={x}是周期函式，其周期為任意正整數，最小正周期是1；
  
• [x]+[y]≤[x+y]≤[x]+[y]+1；
  
• 如果n 正數，則[xn^－1] =[[x]n^－1]
  
• 厄爾米特恆等式：對任意x大於0，恆有
  

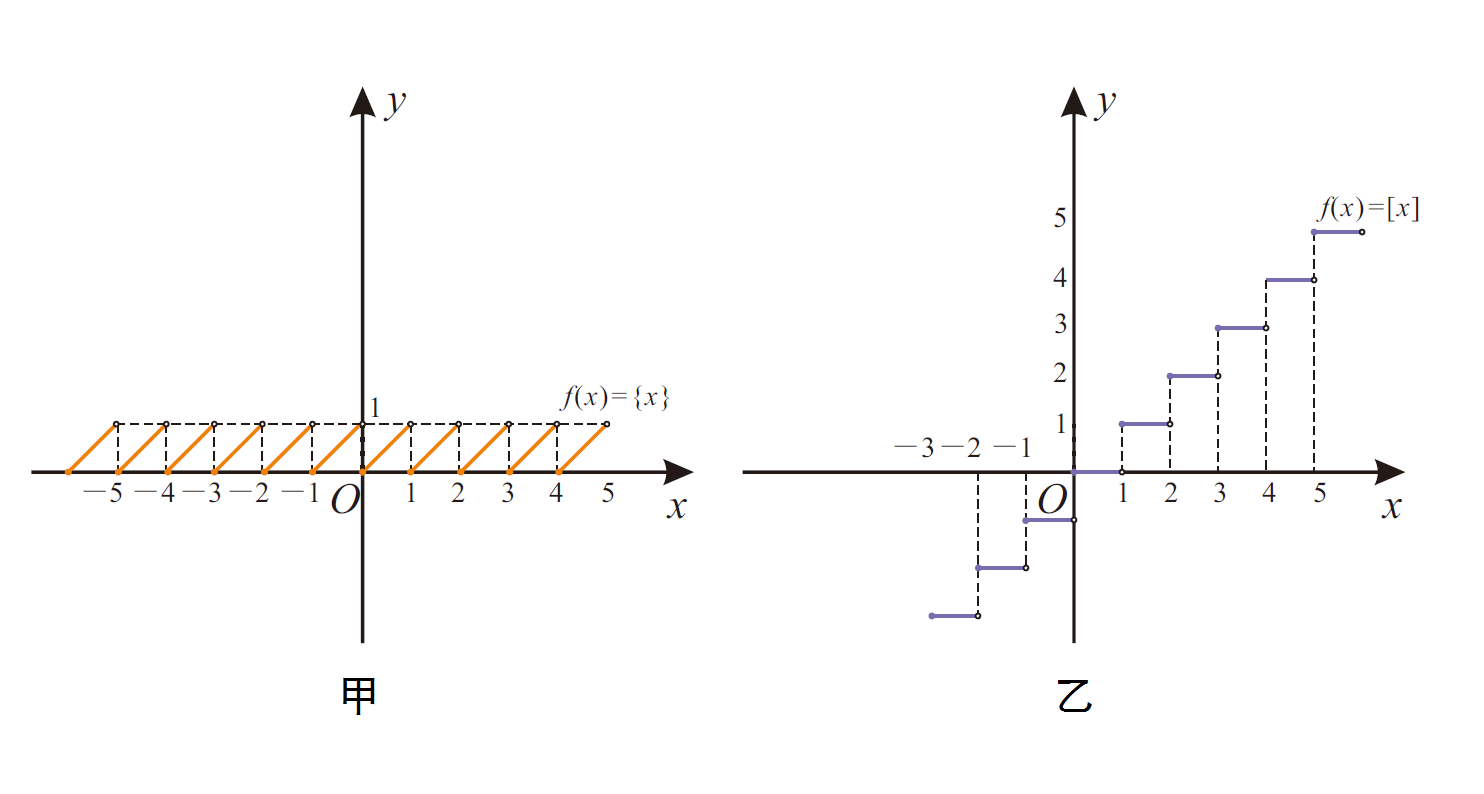
• 函式f(x)={x}，f(x)=[x]圖像如下所示。