基本介紹
- 中文名：體心晶格
- 外文名：body centered lattice
- 類別：非生物
畫法,面心立方晶格,體心立方晶格,性質,氫原子,介紹,計算的結果,結論,
畫法
通過先分解再組合的方法給出面心立方和體心立方晶格第一布里淵區的立體結構，即先確定出一個1/8倒格子晶胞空間對應的第一布里淵區，再將其與另外7個小倒格子晶胞的第 一 布里淵區空間進行組合，最終標識出完整的第一布里淵區結構。
面心立方晶格
設其倒格子晶胞的體心點為O，八個頂角點用 A、B、C、D、E、F、G、H來標註，該面心立方晶格的第一布里淵區應該是這八條由O點出發的體心對角線的垂直平分麵包絡的區域。
畫法思路：1）以體心O為中心點，與八個頂點將該立方體分成8個同等小立方體，大小為OPMN－JKGI；2）畫出1個小立方體的第一布里淵區邊界；3）將八個立方體的布里淵區組合構成完整的布里淵區。
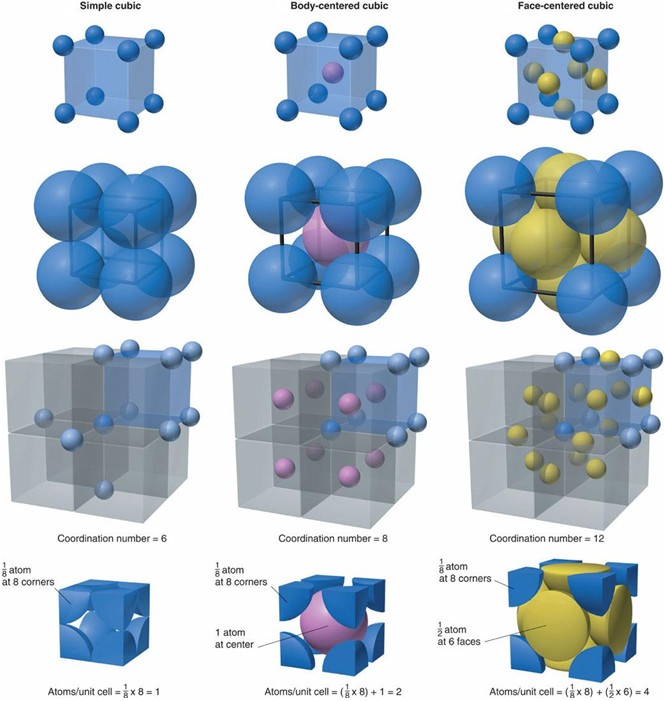
面心立方格子的第一布里淵區是由六個正方形（源於第二布里淵區的限制）及八個正六面體（截八個頂角）包絡的立體區域，常被稱為截角八面體。
體心立方晶格
與求解面心立方晶格第一布里淵區的方法相似，體心立方格子布里淵區的構造首先選取的區域進行部分布里淵區的界定，然後再將各區域的布里淵區進行組合。A點 為1/8區域的頂角，其次近鄰的三個點分別為 C、F和 H，AB長為2π分之a。該區域的第一布里淵區將由 AC、AF和AH線段的垂直平分面所包圍。線段 AC和AF的垂直平分面分別是過DB垂直於ABCD平面的 DBFH平面和過EB垂直於ABEF平面的EBH平面，過ED垂直於EHAD平面的EDCF平面將交於 HB於該立方體的體心O處，連線 EO、BO和DO，所包絡的立體區域則為該1/8立方體的第 一布里淵區，是以等邊三角形EDB為底、AG為高的兩個三稜錐組成。
性質
根據布里淵區的定義，找全正晶格的倒格點是首先要做的工作。從晶體的對稱性出發，在一個倒格子晶胞空間中找到倒格矢垂直平分面的包絡面，再把其餘7個類似的圖形組合在一起構成完整的第一布里淵區的方法，對於像面心立方和體心立方這樣具有高度對稱性的晶體是非常實用的。
氫原子
對於氫原子在 bcc 型過渡金屬 V、C r、Fe、Co 原子簇中處於歪曲、變形的四面體位置和八面體位置的 EH MO 計算結果作一簡要報告。主要是考察氫原子在這兩種環境中的相對穩定性。
介紹
通常情況下，金屬Co具有 hcp ( 六方緊密堆積 ) 結構，但是 WaJmslcy，Thompson，Friedman，White 和Geb alle在金屬 Cr 的基底上製得過Co 的bcc薄層， 在此工作中也把 Co和 V、Gr、 Fe 一 起按 bcc 結構來加以研究。
Hayaashi，Hayamizu 和 Yamamoto 根據脈衝 NMR 的測 ，指出在中氫 子可處於兩種位置，兩者的能量差別 約為o.08ev /原子 ( 8KJ/mol )。
Sugimoto 和 Fukai 推廣了 關於 V、N b、T a 的 量子力學處理的結果，認為氫原子在Fe 中應占據八面體位置。這一預言主要基於Fe 和Cr具有相近的晶格參數，而且實驗上表明氫在 Cr 中以八面體環境更為有利。但並沒有 氫在bcc 一Fe 中位置的實驗結果。
計算的結果
對於每一給定的K值，計算的氫原子結合能 BE( H )都隨著原子序數的增加而減小，即使對於晶格常數相近的Cr 和 Fe 也如此。K值的改變對BE( H )值的影響是不大的，特別對於兩種位置能量差影響更小。例如 T 一位置和O 一位 置BE( H ) 能量的差值在K值增大時，對於V 這個差值分別是 0.12，0.12，0.13cv，對於Cr 分別是0.18， 0.19 和0.19cv。
在過渡金屬氫化物中的氫原子帶有少量的浮負電荷。處於四面體或八面體位置的氫原子算得的淨電荷約為一 0.le， 這個負電荷與金屬 d電子之間的靜電排斥勢將削減氫原子與原子簇之間的結合能。 作為這個靜電勢的適當的量度，可以定義一個“ 相對的d電子排斥勢” ( relative d clectron repulsive potential )，它等於金屬d電子數除以金屬— 氫之間的特徵距離#d/RM-H。對於四面體環境來說，氫原子與緊鄰的四個金屬原子間的距離相同，因而RM-H是確定的。但對於八面體環境，氫原子與緊鄰的六個金屬原子的核間距離是四長兩短，因而需由六個 M 一 H 核間距離取加權平均值來計算#d/RM-H植。
結論
Callaway 用高斯軌道線性組合作的計算，或者用了Kohn 一 sham 一 Gaspar ( KSG ) 的交換勢， 或者用了V on Barth 和 Hedin ( VBH ) 的交換相關勢。Moruzi 等人，則採用了自洽場 Kohn 一 Sham 定域密度近似。所有這三組值都表明，由V 到Co的頻寬值都略有增加，而與這裡 EHMO 的結果相反。這說明 EHMO 這樣的半經驗方法可以求得或預言某種性質的數值，卻不適宜於預言其他的性質 ( 很多方法用變分法處理時也有類似的限制 )。但用優選的K 值求得的頻寬值都有正確的數量級，這表明所用的模型是合理的。
