馮紐曼熵

量子統計力學中，馮諾依曼熵（英語：von Neumann entropy）是經典體系吉布士熵概念的拓展延伸。

基本介紹

• 中文名：馮紐曼熵
• 外文名：von Neumann entropy
• 學科：量子力學術語

數學表示

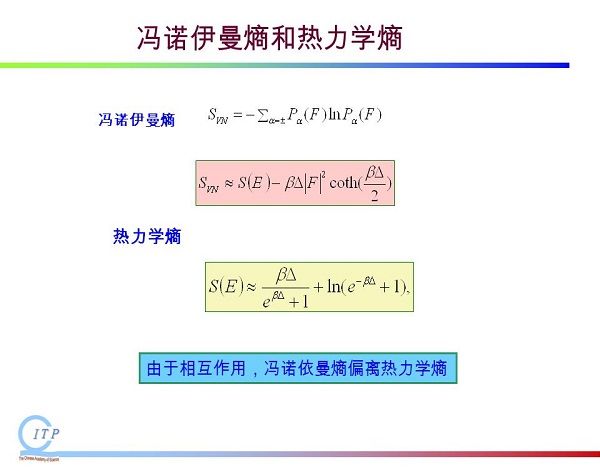
體系的馮諾依曼熵為：

其中 表示求跡， 是體系的密度矩陣。

運用密度矩陣的本徵態向量分解表示

可以得到：

性質

馮諾依曼熵有下列性質：

1) 代表純態；

2) 代表最大混合態，就是所有的 都等於 ，其中 是希爾伯特空間的維數；

對密度矩陣作酉變換， 不變。

3) 馮諾依曼熵是密度矩陣的上凸函式：

4)馮諾依曼熵對獨立體系有加和性，就是：如果 和 是兩個獨立的體系，這樣

套用

馮諾依曼熵在量子資訊理論框架下被廣泛套用於不同的形式（條件熵，相對熵等）。糾纏度量基於與馮諾依曼熵直接相關的一些量。然而，在文獻中已經出現了幾篇關於香農信息量度可能不足的論文，並且因此馮諾依曼熵作為香農熵的適當量子推廣。主要論據是，在經典測量中，香農信息測度是我們對系統性質的無知的一種自然度量，它的存在與測量無關。

相反，量子測量不能聲稱揭示在測量之前存在的系統的性質。這個爭議促使一些作者引入Tsallis熵的非相加性質（標準Boltzmann-Gibbs熵的推廣）作為在量子背景下恢復真實量子信息量度的主要原因，由於Tsallis熵的特殊性，應該描述局部相關性。