馬爾姆奎斯特定理

馬爾姆奎斯特定理是一個有關復域方程解結構的重要定理。1933年，吉田耕作對此定理給出了一個十分漂亮的證明，他的證明用到了奈望林納(Nevanlinna,R.)的近代亞純函式論，因而完全改變了解析理論的面貌。

基本介紹

• 中文名：馬爾姆奎斯特定理
• 外文名：Malmquist theorem
• 適用範圍：數理科學

簡述

馬爾姆奎斯特定理是一個有關復域方程解結構的重要定理。

背景

解析理論的基本定理是柯西的存在惟一性定理，這是一個局部性定理，一旦要求由此經過解析延拓來討論解的大範圍性質，就會出現非常複雜的情況。一個重要的問題是，微分方程何時具有整個複平面上的單值亞純解或有限多值代數體函式解。

對於如下形式的方程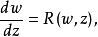

其中R(w,z)為w與z的有理函式z的有理函式。1913年，馬爾姆奎斯(Malmquist,J.)首先得到了一個極為重要的結果，被稱為馬爾姆奎斯特定理。

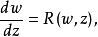
具體內容

該定理斷言：在上述方程中，設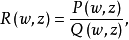

其中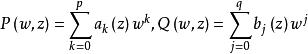

是w的互質多項式，係數{a_k(z)}和{b_j(z)}是z的有理函式。

若存在非有理分式的亞純解，則必q=0，p≥2，即方程退化為黎卡提方程

其中a,b,c為z的有理函式。

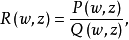
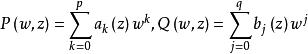
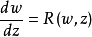
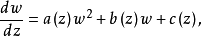
意義

此後發展的事實，馬爾姆奎斯特定理的意義則遠遠超過了此定理本身。

1933年，吉田耕作對此定理給出了一個十分漂亮的證明，他的證明用到了奈望林納(Nevanlinna,R.)的近代亞純函式論，因而完全改變了解析理論的面貌。

馬爾姆奎斯特定理因此得到推廣和精確化。